Tristan Leclercq, Departement of Mechanics, LadHyx-CNRS, Ecole Polytechnique, gives a seminar on "Drag reduction by elastic reconfiguration with dynamics"
organized by the Department of Aerodynamics, Aeroelacticity and Acoustics of ONERA in Meudon.
The slides of the talk are available here.
Drag reduction by elastic reconfiguration with dynamics
Séminaire de site ONERA/DAAA – Centre de Meudon
Tristan Leclercq
Department of Mechanics, LadHyx-CNRS, Ecole Polytechnique
- Octobre 2017 – 11h - Salle AY-02-62
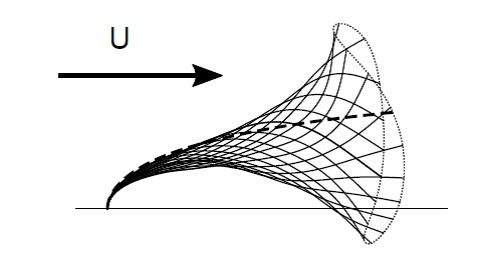
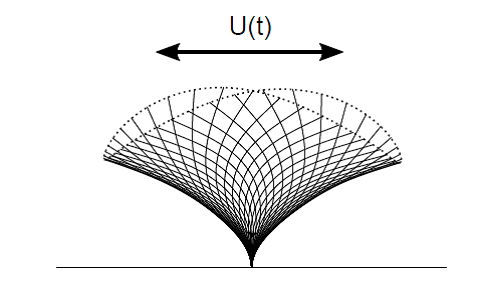
Figure 1 – Snapshots of the dynamic deformation of a flexible cantilever plate in a transverse flow (solid lines) and trajectory of the tip (dotted lines) , in two different situations. (Left) Flutter of a deflected beam in steady flow. Static equilibirum shape superimposed (dashed line) - (Right) Dynamics reconfiguration in an oscillatory flow
When flexible structures are placed in a fluid flow, the drag they experience is strongly modified by the deformation caused by that flow. In particular, the work of [1] has shown that plants in nature benefit from their flexibility because the drag they have to withstand is lower than it would be if they were rigid. This ability to reduce flow-induced forces by passively adapting its static equilibrium shape is now thought to be a key factor allowing aquatic organisms to survive in flow-dominated habitats [2]. To better understand this phenomenon and quantify the amount of drag reduction resulting from the deformation, several authors have studied the mechanism of elastic reconfiguration in the idealized context of a uniform and steady flow [1, 2].
However, if flexible structures can vary their static shape, they are also given the ability to move dynamically within the flow. Such motion is responsible for additional inertial forces, and it is unclear whether the total drag would be reduced or enhanced when dynamical reconfiguration occurs. I will address this question by considering a flexible cantilever Euler-Bernoulli beam, clamped transverse to the flow, in two different situations where dynamics is involved. Firstly, I will discuss the case where the background flow is steady and structural dynamics is self-triggered. As deflection becomes larger, the structure progressively aligns with the flow and may become subject to the same flutter instability as flags (see Figure 1a). Secondly, I will present the situation where the background flow itself is oscillating (see Figure 1b). Depending on the amplitude of the oscillations, different kinematic regimes are observed for the structural response, associated with different scaling laws for the total drag.
References:
[1] S. Vogel. « Drag and flexibility in sessile organisms », American Zoologist, 24(1):37-44, 1984.
[2] D. L. Harder, O. Speck, C.L. Hurd and T. Speck, « Reconfiguration as a prerequisite for survival in highly unstable flow-dominated habitats », Journal of Plant Growth Regulation, 23(2):98-107, 2004.
[3] S. Alben, M. Shelley, and J. Zhang, “How flexibility induces streamlining in a two-dimensional flow, Physics of fluids, 16(5):1694-1713, 2004.
[4] F. Gosselin, E. de Langre and B.A. Machada-Almeida, « Drag reduction of flexible plates by reconfiguration », Journal of Fluid Mechanics, 650, 319-341, 2010.
