The control of the vibration of an elastic splitter plate clamped on a rigid circular cylinder is investigated here. The originality of the proposed methodology is to suppress the vibration of the elastic splitter plate by stabilizing the unstable eigenmode responsible for the vibrations. A similar methodology was successfully applied to the control of vortex shedding behind a circular cylinder, i.e. by stabilizing the unstable hydrodynamic eigenmode associated to the vortex shedding. In the present work, we have extended this methodology to fluid/structure problems, i.e. by stabilizing the unstable hydroelastic eigenmode responsible for the structural deformations and flow unsteadiness. Passive control strategies are considered, meaning that no additional energy is provided by the control to the system.
with shunted piezo-electric patches
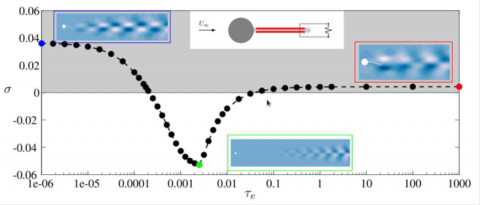
In view of considering a realistic way of controlling vibrations of elastic splitter plates, two piezo-electric patches embedded at the top and bottom of the elastic plate are considered. The piezo-electric patches are modeled as proposed by … and an electrical resistance is added to connect them in a serial circuit (shunted configuration). To model the dynamic of this fluid-solid-electric system, an additional equation governing the electric state is added and coupled to the fluid-solid equations that govern the dynamic of the elastic plate immersed in the fluid. Self-sustained instabilities of the coupled fluid-solid-electric configurations are investigated, by linearizing the equations around the steady solution and by determining the leading eigenvalues of the fluid-solid-electric Jacobian matrix. When varying the electrical resistance connecting the piezo-electric patches, a stabilization of the initially unstable eigenmode is achieved for certain values of the electrical resistance. However, the destabilization of a new eigenmode is also observed when too large values of the electrical resistance are considered.
by shape-optimization of the rigid structure
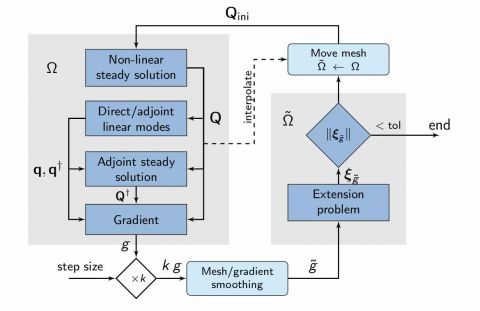
A second way of controlling passively the flow-induced elastic instability is to change the shape of the rigid cylinder which supports the elastic plate. The optimization of the cylinder shape aims at stabilizing the unstable eigenvalue, shown in the figures below. As the algorithm goes on, the growth-rate of the coupled fluid-structure eigenvalue (represented on the right panel on the figure below) is decreased until it reaches the target value (represented with the red dashed line). On the left panel, the evolution of the shape is represented, together with the vector field materializing the deformation fields that modifies the shape.
Ref : G. Allaire. Conception optimale de structures. Springer. 2007, T. Nakazawa and H. Azegami, Shape optimization of flow field improving hydrodynamic stability, Jap. Jour. Ind. App. Math, 2016, 33:167-181
The minimization algorithm is a descent method, the gradient vector being obtained with the adjoint fields of the steady equation and of the fluid-structure linear eigenvalue equations. To enhance the regularity of the shape, smoothing procedures are also implemented when the gradient information is used to deform the domain.