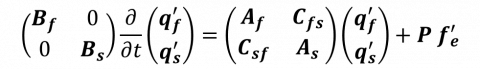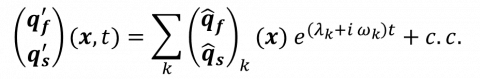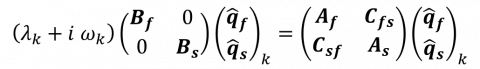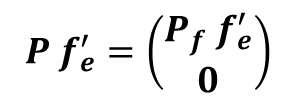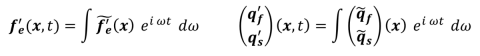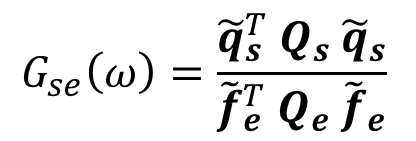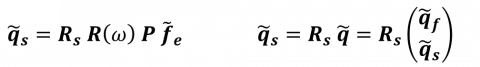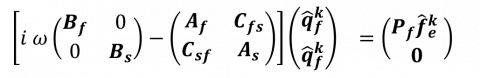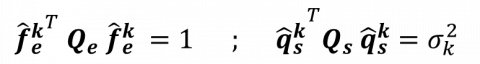Whatvever the method used to couple the fluid and structural dynamics (Arbitrary Lagrangian Eulerian versus Fictitious Domain) the linearized equations of the fully coupled problem can be formally written
where the fluid and solid component are denoted with the subscript f and s. When considering the ALE formulation, the extension displacement is included in the fluid component. The operators on the diagonal of the right hand-side operator represent the intrinsic fluid and solid dynamics, while the off-diagonal operators represent the fluid-solid coupling operators coming from the linearization of the velocity and stress continuity. An external forcing term denoted  is included in the perturbation so as to investigate the linear response of the fluid-structure system to external perturbation.
is included in the perturbation so as to investigate the linear response of the fluid-structure system to external perturbation.
Two types of solutions for the above equations can be scrutinized depending on the fluid-structure configuration of interest. The homogeneous solution of the above equation is of interest when investigating a self-sustained fluid-structure instability. Since we are more specifically interested by homogeneous perturbations that grow at large time, a modal analysis detailed below is then performed. On the other hand, when the homogeneous perturbation decays to zero at large time, solutions of the non-homogeneous problem are interesting to analyze. The resolvent analysis detailed below allow to determine the optimal external excitation that lead to the largest energetic amplification in the fluid-structure system.
Modal analysis
Vortex-induced vibrations, coupled mode flutter, static divergence or stall flutter are flow-induced instabilities that arise spontaneously when coupling a fluid and a structure. These self-sustained flow-induced structural instabilities are investigated by examining the long-term temporal behavior of the linear perturbation. This temporal behaviour is conveniently described by assuming a modal decomposition of the perturbation
where the behaviour of every mode is assumed to be exponential in time, with a growth rate given by ![]() and a frequency given by
and a frequency given by  . Once injected into the linearized equations above (with an external forcing equal to zero), the modes are found as eigenvectors of the following fluid-structure eigenvalue problem
. Once injected into the linearized equations above (with an external forcing equal to zero), the modes are found as eigenvectors of the following fluid-structure eigenvalue problem
where the complex eigenvalue gives the associated growth rate (real part) and frequency (imaginary part). By determining the leading eigenmode of the linear fluid-structure operator, i.e. the eigenmode of largest growth rate, we can analyze the long term behaviour of fluid-structure perturbations.
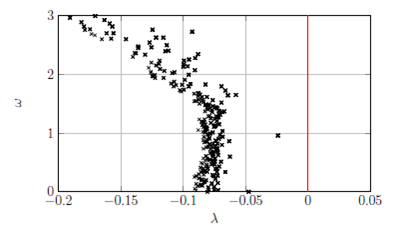
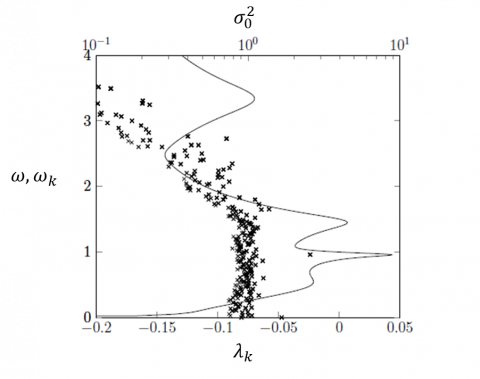
A typical output of the modal analysis is the eigenvalue spectrum displayed in the figure beside. All of the eigenvalues, denoted by crosses, lie in the left half-plane, i.e. they have a negative growth rate. Therefore the underlying steady fluid-structure solution is stable. It will get unstable when at least on eigenvalue crosses the red line.
Such modal analysis have been applied to most of the fluid-structure problem that we have investigated up to now in the project, i.e. the vortex-induced vibration of spring-mounted rigid cylinder, the flutter analysis of elongated plates in turbulent flows, the flow-induced elastic instabilities of flexible flags and the flow-induced elastic instabilities of splitter plates clamped on a rigid cylinder.
Resolvent analysis
Vibrations and deformations of structures are not necessarily induced by self-sustained mechanisms. Insteady they can result from an external excitation, such as incoming perturbations in the flow or external excitation of the elastic structure. In such cases, the long-term behavior of the perturbations is not of interest anymore, unlike the frequency response (or impulse response) of the perturbation equations. Generally speaking, the resolvent analysis of a linear system consists in determining externals excitation leading to largest linear responses for a given frequency. in purely hydrodynamics problems, the resolvent analysis was successfully applied (by repeating this analysis for various frequencies) to investigate convective flow instabilities without assuming the parallelism of the underlying base flow. For instance the Tollmien-Schlichting waves developing in a zero pressure-gradient laminar boundary layer flow can be captured as the leading resolvent mode of the linear hydrodynamic operator. Such analysis is extended in this project to fluid-structure interaction problems, for which various source of excitation as well as various response of the fluid-structure system can be considered. We are mainly interested to investigate the optimal source of excitation in the fluid that lead to the largest displacement of structures. To that aim, the action of the prolongation operator P is defined as
so that the external forcing only acts as a source term in the fluid momentum equations. Assuming a Fourier decomposition of the external forcing as well as the fluid and solid response,
yields to the following frequency response problem
where  is the resolvent operator of the fluid-structure problem. To investigate the optimal source of excitation in the fluid that lead to the largest displacement of structures at a fixed frequency
is the resolvent operator of the fluid-structure problem. To investigate the optimal source of excitation in the fluid that lead to the largest displacement of structures at a fixed frequency  , we introduce two scalar products
, we introduce two scalar products
to define a norm in the space of the solid response and a norm in the space of the external forcing. The matrix Qs is for instance defines so that the associated norm measures the displacement of the solid response. The gain is then defined as the ratio between the norm of the solid response and the norm of the external forcing
Then, we wish to find the external forcings that maximize this gain. To do so, it is first convenient to clearly write the relation between the external forcing (input) and the solid response (ouput) as
where Rs is a restriction operator that selects the structural component of the fluid-solid response. The numerator can then be rewritten as a function of th external forcing as
The resolvent analysis consists in determining the eigenvalues of the operator shown in blue. Since this operator is symmetric, its eigenvalues are real and positive. The eigenvalue problem then writes
where the positive eigenvalues are ordered as follows  and the corresponding eigenmodes are the optimal and sub-optimal external forcings. The fluid-structure responses to these external forcings are obtained by solving the frequency problem
and the corresponding eigenmodes are the optimal and sub-optimal external forcings. The fluid-structure responses to these external forcings are obtained by solving the frequency problem
If the external forcing eigenmode are normalized so that their norm is unitary, the eigenvalues then represent the squared norm of the structural response
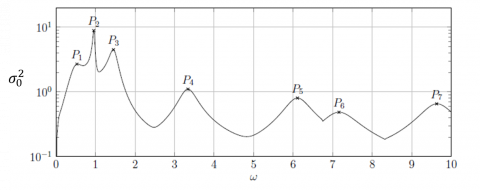
A typical ouput of the resolvent analysis is a plot of the largest (optimal) eigenvalue as a function of the forcing frequency, as displayed in the figure below.
Several peaks are observed at various frequency. A comparison of the modal and resolvent analysis clearly shows that the peaks of energy obtained with the resolvent analysis do not necessarily correspond to the existence of an eigenvalue close to the forcing frequency. This is due to the non-normality of the fluid-structure operator.
This fluid-structure resolvent analysis has been first applied to a wing composed of a rigid leading edge and a flexible trailing edge (see the master thesis of Georg Lopez).
It is currently applied to investigate the interaction of boundary-layer flow waves with flexible elements, such as pillars clamped on a rigid wall or cavity filled in with an elastic material.