The Distributed-Lagrange-Multiplier Fictitious-Domain approach was originally introduced by Glowinski et al (1999) to describe the motion of rigid particles immersed in an incompressible fluid. This formulation was then extended by Yu (2005) to take into account the interaction of elastic structures with an incompressible fluid.
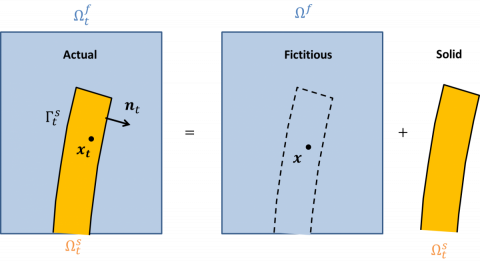
As shown with the scketch above, the fictitious-domain approach consists in deriving equations written in a fixed domain, composed of the fluid domain and a fictitious domain filled in with fluid, that still remain valid for describing the fluid and solid motions. The Eulerian Navier-Stokes equations governing the fluid dynamics are modified in the fictitious domain so as to take into account the presence of the deformed solid domain. Following Glowinski et al (1999) and Yu (2005), distributed source term are added to the momentum equations and computed so that the constraint of equality between the fluid and solid velocity is fulfilled in the fictitious domain. TRhese diretibuted forcing are often referred to as the disttribueted Lagrange multipliers as they are introduced to mathematically impose additional contraints.
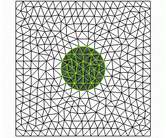
The main advantage of such method compared to the ALE formulation relies in the Eulerian description of the fluid dynamics, even if additional source terms need to be introduced. On the other hand, this method is a non-conforming method, in the sense that, once the problem is spatially discretized, the fluid-structure interface spreads accross mesh elements, as shown in the animation beside.
Starting from the fictitious formulation of the nonlinear fluid-structure euqations, we have derived the perturbed equations and investigate the modal analysis in various fluid-structure condifuration.
- Rigid structures
The vortex-induced vibrations of a spring-mounted cylinder have been first investigated with the fictitious domain approach so as to validate the implementation in case of a rigid structure.
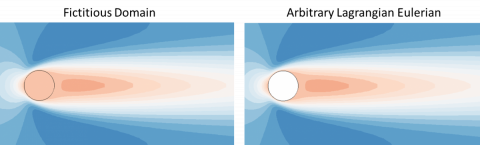
The figure above show the streamwise velocity of the steady solution obtained with the Fictitious Domain approach and the Arbitrary LAgrangian Eulerian approach. The solutions are very similar execept very close to the cylinder's wall. Small discrepancies between the two solutions are observed due to oscillations of the velocity filed in the fictitious domain solutions. This phenomenon is also observed when the interface of the fictitious domain conforms with the interface of the solid domain.
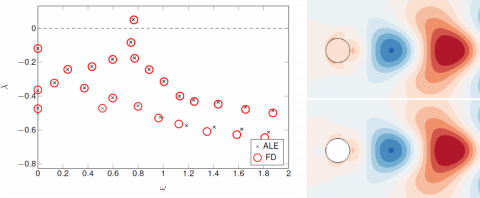
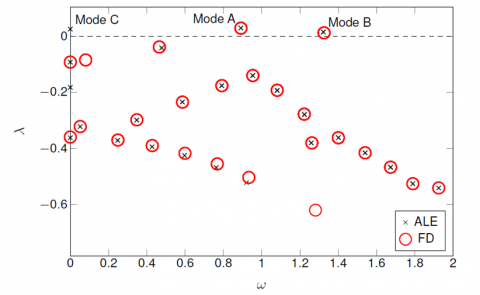
The eigenvalue spectrum of the modal analysis, displayed in the figure above, are very similar using the two formulations, as well as the unstable eigenmodes.
- Elastic structures
The flow-induced deformation of the elastic splitter plate has then been investigated with the fictitious domain approach so as to validate the implementation with an elastic structure, by comparison with the ALE formulation.
The fluid and solid non-dimensional parameter have been chosen to obtain three unstable eigenvalues with the ALE formulation
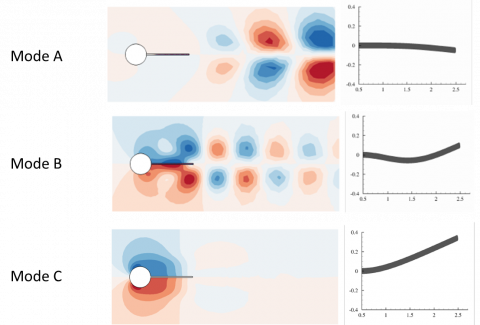
The two unsteady modes (A and B) are well captured with the fictitious approach. The so-called mode A is a vortex-induced deformation mode and the displacement of the splitter plate looks like a one-node bending mode. The so-called mode B is characterized by a higher-frequency and the structural displacement of the splitter plate looks like a two-node bending mode.
The steady mode C, which is unstable with the ALE formualtion, is not captured with the fictitous domain formulation. The physical mechanism for this steady mode can be attributed to negative fluid-induced stiffness that counterbalances the elastic restoring forces. We believe that this fluid-induced stiffness is not well reproduced by the fictitious domain approach, as the fluid-solid interface is not accurately described by this non-conforming method. To confirm such results, we are currently investigating the static divergence of a spring-mounted alongated plates with the fictitious domain approach.
► More about our work in Assessment of Fictitious Domain method for Linear Stability Analysis of Fluid-Structure systems (ERCOFTAC-SIG33, 2017, Siena)
References:
R. Glowinski, T-W. Pan, T.I. Hesla, D.D. Joseph., J.Périaux. A distributed Lagrange multiplier/fictitious domain method for flows around moving rigid bodies: Application to particulate flow. Int. J. Numer. Meth. Fluid, vol 30, pp. 1043-1066, 1999.
Z. Yu. A dlm/fd method for fluid/flexible-body interaction, JOurnal of Computational Physics, vol 207, pp. 1-27, 2005.