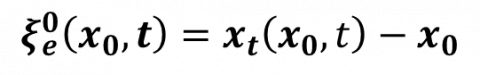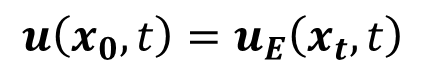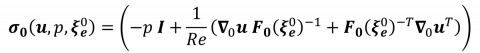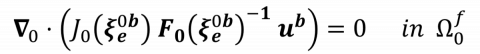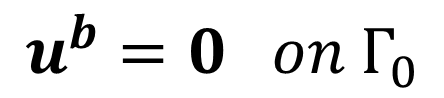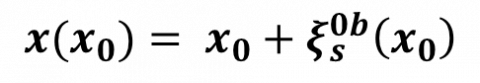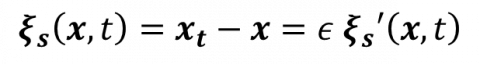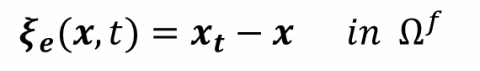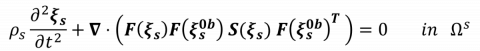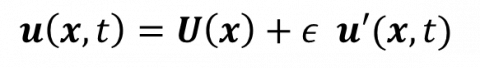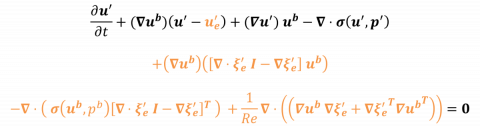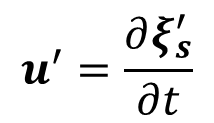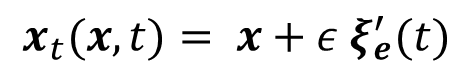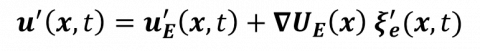Rigorous linearizations of Aribitrary Lagrangian Eulerian (ALE) formulations for fluid-structure interaction problems were first performed at the beginning of the century by Fanion et al (2000) [1], Lesoinne et al. (2001) [2] and Fernandez & Le Tallec (2003) [3,4]. At least two linearized formulations were obtained, depending on the choice of the perturbative decomposition for the fluid velocity. After recalling the ALE formulation of the nonlinear Navier-Stokes equations, the derivation of the linearized equations is detailed, by introducing perturbative decompositions of either the Lagrangian fluid velocity or the Eulerian velocity.
Arbitrary Lagrangian Eulerian (ALE) method
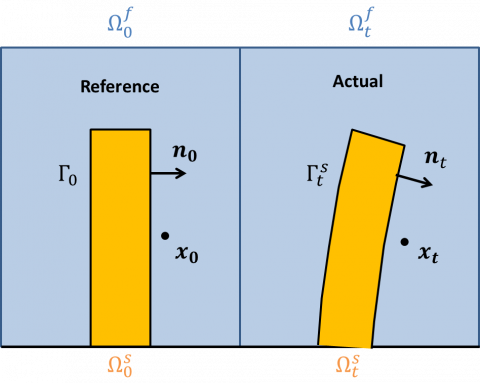
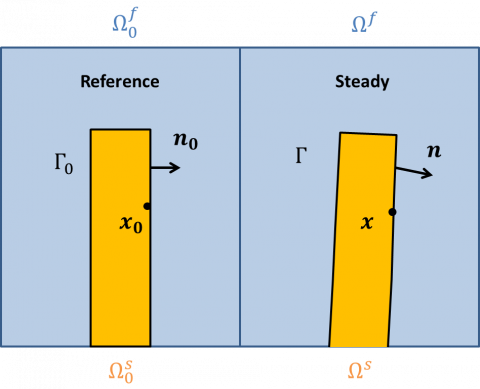
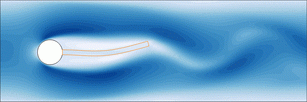
The Arbitrary Lagrangian Eulerian method is a conforming method. The fluid domain (depicted in blue in the figure below) is deformed in order to conform with the solid domain (in orange) at the fluid-solid interface.
Similarly to the description of the solid dynamics, the motion of the fluid domain is described in a Lagrangian setting. The extension displacement field  is introduced to track a position in the actual fluid domain with respect to a position in the reference fluid domain, i.e.
is introduced to track a position in the actual fluid domain with respect to a position in the reference fluid domain, i.e.
Unlike the solid displacement field  , the extension displacement field does not represent a physical quantity. It is governed by an arbitrary equation which is introduced so as to propagate the displacement of the fluid-solid interface into the fluid domain. The fluid motion is then described by the so-called Lagrangian fluid velocity field, denoted
, the extension displacement field does not represent a physical quantity. It is governed by an arbitrary equation which is introduced so as to propagate the displacement of the fluid-solid interface into the fluid domain. The fluid motion is then described by the so-called Lagrangian fluid velocity field, denoted  and defined into the reference configuration as
and defined into the reference configuration as
which states that the Lagrangian fluid velocity at the position in the reference configuration is equal to the Eulerian fluid velocity at the position
in the reference configuration is equal to the Eulerian fluid velocity at the position  in the actual fluid domain. For an incompressible flow, this Lagrangian fluid velocity is then governed by the following Arbitrary Lagrangian Eulerian formulation of the momentum equation is
in the actual fluid domain. For an incompressible flow, this Lagrangian fluid velocity is then governed by the following Arbitrary Lagrangian Eulerian formulation of the momentum equation is
where the Cauchy stress tensor is defined as
The deformation gradient tensor associated to the extension displacement, its determinant and the fluid mesh velocity are defined as
are defined as
The ALE formulation of the divergence-free condition for an incompressible fluid is
Steady solutions and configuration
Equilibrium solutions of the fluid-structure interaction problem are solutions for which the fluid loads exactly balance the elastic forces, so that the fluid-solid interface does not move. They are obtained as solutions of the nonlinear steady ALE equations written in the reference configuration. The steady Lagrangian fluid velocity  , fluid pressure
, fluid pressure  , solid displacement
, solid displacement  and extension displacement
and extension displacement  satisfy the following equations:
satisfy the following equations:
- Steady equation for the fluid momentum and mass conservation
Note that the fluid mesh velocity vanishes in the steady momentum equation since the extension displacement does not depend on time.
- Steady nonlinear elastic equation
- Continuity of the fluid and solid stresses
- Continuity of the fluid and solid velocity
The above equations are written in the reference configuration. The steady-state solution that solves these equations enables to define a new time-independent configuration, the so-called steady configuration shown in the scketch below.
The stability of the steady-state solution can be investigated by linearizing the nonlinear ALE equation formulated either in the reference configuration or in the steady configuration.
Linearization of the ALE formulation in the reference configuration
The solid and extension displacements are decomposed as
By introducing these decompositions (and the decomposition of all the other variables) into the nonlinear ALE formulation written in the reference configuration, we obtain linearized equations in which some terms are proportional to the steady gradient deformations. These terms can be removed from the linearized equations by choosing the steady configuration as a new reference configuration.
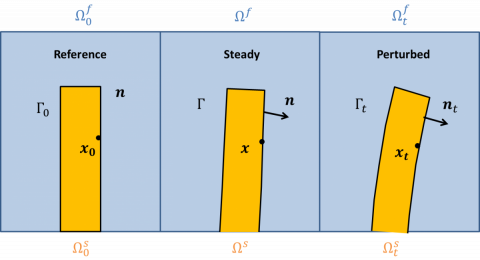
To clarify this, let us consider a position  in the perturbed (solid) domain. It can be expanded as
in the perturbed (solid) domain. It can be expanded as
where the first equality is the decomposition in the reference configuration. The second equality is the decomposition in the steady configuration, where the position  in the steady configuration is given by
in the steady configuration is given by
While the displacement defined in the reference configuration  is the sum of a steady and a perturbative component, the displacement defined in the steady configuration has solely a perturbative component, i.e.
is the sum of a steady and a perturbative component, the displacement defined in the steady configuration has solely a perturbative component, i.e.
The steady components of the displacement variables defined in the steady configuration being strictly equal to zero, all the terms proportional to the steady gradient deformation in the linearized equations will vanish.
ALE formulation in the steady configuration
Stepping back to the nonlinear equations, the ALE formulation of the Navier-Stokes equations is written in the steady configuration as
where the Lagrangian fluid velocity is still denoted but now depends on the steady position, and
but now depends on the steady position, and  is the extension displacement field defined in the steady configuration as
is the extension displacement field defined in the steady configuration as
While the above formulation of the fluid equation is barely changed, the formulation of the solid elastic equation is modified as
Linearization of the ALE formulation in the steady configuration
The solid and extension displacements are now decomposed as
where the steady displacements are now strictly equal to zero and thus the displacements are only at the perturbation level.
- Lagrangian decomposition and perturbative formulation
The Lagrangian decomposition is a classical decomposition of the Lagrangian velocity field into a steady component and an infinitesimal unsteady component
By introducing such decomposition into the ALE formulation of the fluid momentum equation written in the steady configuration, we obtain
The terms in black form the classical perturbation equations in hydrodynammics, while the orange terms are additional terms that depend on the (perturbative) displacement of the fluid domain. These additional terms come from the linearization of the convective operator (second line) and of the fluid stress (third line).
At the fluid-structure interface, the continuity of the fluid and solid perturbative velocities is classically epxressed as
while the continuity of the perturbative fluid and solid stress is expressed as
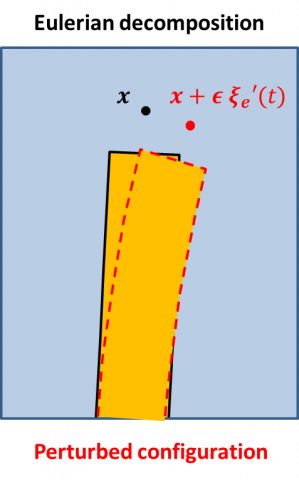
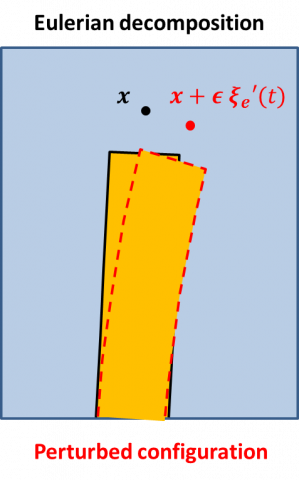
- Eulerian decomposition and perturbative formulation
The Eulerian decomposition is a decomposition of the Eulerian velocity field into a steady component and an infinitesimal unsteady component,
that takes into account the decomposition of the spatial position in the fluid domain as
where x indicates the time-independent position of the steady configuration. Due to the equality of the (total) Lagrangian and Eulerian velocities, the Lagrangian and Eulerian perturbations are related through
which shows that the Lagrangian fluid perturbation is the sum of the Eulerian fluid perturbation and a perturbation proportional to the extension displacement. Since the extension displacement is induced by the solid displacement of the fluid-solid boundary, the second term is an extrinsic fluid perturbation induced bu the solid displacement, unlike the first term that is an intrisinc fluid perturbation.
By introducing such decomposition of the fluid perturbation, yields, after tdious computatinio, to the following perturbative formulation:
References :
J. Donea, A. Huerta, J-P. Ponthot, A. Rodriguez-Ferran. Arbitrary Lagrangian-Eulerian Methods. Enc. Comp. Mech, 2004, chap.14.
► More about our work in Fluid-structure stability analysis of flexible splitter plates (EFMC, 2016, Sevilla).
This animation should be changed or shoud go into the numerical part.
When it comes to investigate the stability of fluid-structure systems, the simplest approach consists in assuming that the perturbation of the equilibrium only affects the velocity interface condition between the fluid and the solid, in the sense that at the interface, the motion of the solid might be approximated by only a transpiration velocity proportional to the solid displacement. For aeronautical applications, this approach is often referred as the transpiration method [1] and has been widely and successfully used in aeroelasticity analyses.
However, a rigorous derivation of this formulation showed that in addition to the modified velocity conditions at the interface, extra terms should be considered in the most general case to take into account the modification of the stress interface condition as well. These terms arise as higher-order derivatives of the stationary equilibrium solution at the fluid-solid interface, which might lead to numerical difficulties. For that reason, we choose to derive a stability formulation from the Arbitrary Lagrangian Eulerian equations describing the fluid-solid interaction, written in a reference configuration chosen as the steady equilibrium.
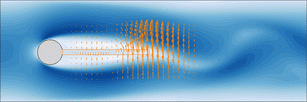
This approach is illustrated on the figure above. The fluid-solid system as is could be observed in a laboratory experiment (left), is recasted in a fixed domain by means of a variable change represented by the orange arrows on the figure on the right side. This procedure allows an easier linearization of the system, since the domain is not moving anymore. Depending on the decomposition chosen for the perturbation, one obtains the classical transpiration stability equations [1] or our formulation that shows better convergence properties at a moderate computational effort increase.
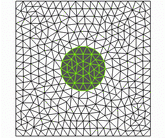
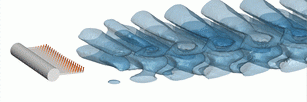
A consistent linearized system is finally obtained, which describes the evolution of small perturbations of a steady fluid-solid equilibrium in a fully coupled fashion. It is then possible to determine the asymptotic stability of the linearized system (global stability approach [4], see for instance a fluid-structure mode below) or evaluate the response to external perturbations [5], by extending appraches initially designed for the analysis of pure fluid sytems to the fluid-structure case.
References:
[1] T. Fanion, M.A. Fernandez, P. Le Tallec. Deriving adequate formulations for fluid-structure interactions problems: from ALE to Transpiration. Revue Européenne Des Eléments Finis, vol. 9, pp 681-708, 2000.
[2] M. Lesoinne, M. Sarkis, U. Hetmaniuk & Charbel Farhat. A linearized method for the frequency analysis of three-dimensional fluid/structure interaction problems in all flow regimes. Comput. Methods Appl. Mech. Engrg., vol. 190, pp 3121-3146, 2001.
[3] M.A. Fernandez, P. Le Tallec. Linear stability analysis in fluid-structure interaction with transpiration. Part I: Formulation and mathematical analysis. Comput. Methods Appl. Mech. Engrg., vol. 192, pp 4805-4835, 2003.
[4] M.A. Fernandez, P. Le Tallec. Linear stability analysis in fluid-structure interaction with transpiration. Part II: Numerical analysis and applications. Comput. Methods Appl. Mech. Engrg., vol. 192, pp 4837-4873, 2003.
[5] D. Sipp, O. Marquet, P. Meliga, A. Barbagallo. Dynamics and control of global instabilities in open-flows : a linearized approach. App. Mech. Rev., 2010, 63.
[6] P. Schmid. Nonmodal stability theory, Annu. Rev. Fluid. Mech. 2007, 39.