Please report any problems to Clément Roos (croos@onera.fr). We will try to fix them as quickly as possible!
Overview
The APRICOT library (Approximation of Polynomial and Rational-type for Indeterminate Coefficients via Optimization Tools) of the SMAC toolbox allows numerical data to be converted into simple yet accurate polynomial or rational expressions. Approximants are obtained, for which the number of terms in the numerator and denominator is as low as possible. The motivations for generating sparse expressions are twofolds. First, it is a natural way to prevent data overfitting and to ensure a smooth behavior of the model between the points used for approximation. Then, it allows to get simple LFR which are tractable for analysis and design purposes. The proposed tools can be used to get an LFR from a set of scalar, vector or matrix samples. More information about the underlying algorithms can be found in [8,9,4].
Motivations
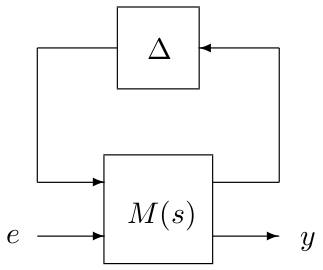
A Linear Fractional Representation (LFR) is a model where all known and fixed dynamics of a given system are put together in a linear time-invariant plant $M(s)$, while the uncertain and varying parameters are stored in a block-diagonal matrix $\Delta$ (see Figure 1). LFR modeling is a widely spread and a very efficient tool in the fields of system analysis and control design. It notably allows to evaluate the robustness properties of uncertain closed-loop plants (e.g. using $\mu$-analysis, IQC or Lyapunov-based methods), and to design robust control laws (especially using $H_\infty$ approaches) or gain-scheduled controllers. But the efficiency of the aforementioned analysis and synthesis techniques strongly depends on the complexity of the considered LFR, which is measured in terms of both the size of the matrix $\Delta$ and the order of the plant $M(s)$. An increase in complexity is usually source of conservatism, and can even lead to numerical intractability.
In most industrial applications, physical systems are described using a mix of nonlinear analytical expressions and tabulated data. Therefore, a two-step procedure has to be implemented to obtain a suitable LFR: a linear model with a polynomial or rational dependence on the system parameters is first generated, and then converted into a linear fractional form. Several techniques such as object-oriented realization exist to perform the latter transformation. Although the minimality of the resulting LFR cannot be guaranteed, symbolic preprocessing techniques as well as numerical reduction usually permit to overcome complexity, and efficient softwares such as the GSS library of the SMAC toolbox and the LFR toolbox are available [1]. On the other hand, the preliminary issue of converting the tabulated or irrational data into simple yet accurate polynomial or rational expressions has been paid much less attention, although it is of significant practical importance. In the aeronautic field for example, most aircraft models include tabulated aerodynamic coefficients determined by CFD (Computational Fluid Dynamics), wind tunnel experiments or flight tests, and several controller gains depend on the flight parameters in a tabulated fashion. The motivations for developing enhanced computational tools dedicated to tabulated data approximation are twofold. The first one is of physical nature. Computing rational expressions with sparse structure, for which the number of terms in the numerator and denominator is as low as possible, is a natural way to prevent data overfitting and to ensure a smooth behavior of the model between the points used for approximation. On the other hand, building an LFR from a polynomial or a rational expression $f(x^1,\dots,x^n)$ results in a block diagonal matrix $\Delta=\textrm{diag}(x^1I_{p_1},\dots,x^nI_{p_n})$. The number $p_j$ of repetitions of each parameter $x^j$ in $\Delta$ is strongly linked to the number of occurrences of $x^j$ in $f$. Indeed, although this is not an exact rule, the trend is as follows: the fewer the occurrences of $x^j$ in $f(x^1,\dots,x^n)$, the smaller the size of $\Delta$. In other words, no matter how efficient the LFR generation tools can be, they are of little help if the rational expressions to be converted are unnecessarily complex. Hence, the need to get tractable LFR for analysis and design purposes is another strong motivation for generating sparse rational expressions. For a given accuracy, an intuitive idea is to determine a rational function for which the numerator $P$ and the denominator $Q$ are two polynomials of the lowest possible degrees. This fairly simple strategy is followed by most existing methods. A classical linear least-squares technique is usually applied in case the rational function is restricted to be polynomial [1]. In the general case, a nonlinear least-squares technique can be implemented to minimize the approximation error [2], whereas a Quadratic Programming problem can be solved to ensure that the resulting rational function intersects a set of intervals containing the data [3]. But all these techniques suffer from the same drawback: all admissible monomials of $P$ and $Q$ are usually nonzero, regardless of their real ability to model the data. More generally, the question of which terms should be included in the model is often addressed by trial-and-error, or even ignored in practice. A way to deal with this question is to use orthogonal least-squares, which allows to evaluate the ability of each monomial to efficiently model the data and therefore to select only the most relevant ones, leading to sparse expressions. This approach is applied by [4,5,6,7] to model aeronautical data with polynomials, but until recently, practical methods leading to rational expressions were still missing. Yet, the additional degrees of freedom offered by such expressions could lead to simpler expressions and thus to smaller LFR. In this context, two algorithms have recently been developed to compute rational expressions with sparse structure, i.e. with as few monomials in $P$ and $Q$ as possible: a direct approach computing a rational approximant in a single step thanks to a symbolic regression technique is proposed in [8], while an indirect approach creating a rational model by means of an intermediate surrogate modeling is introduced in [9]. Most of the aforementioned algorithms are implemented in the APRICOT library of the SMAC toolbox.
Generation of an LFR from a set of scalar, vector or matrix samples
Let $\left\{y_k\in\mathbb{R}^{n_1\times n_2}, k\in [1, N]\right\}$ be a set of samples (measurements, tabulated data...) obtained for different values $\left\{x_k\in\mathbb{R}^n,k \in [1, N]\right\}$ of some explanatory variables $x\in\mathbb{R}^n$. The purpose of the APRICOT library of the SMAC toolbox is to compute a rational function $f: \mathbb{R}^n\rightarrow\mathbb{R}^{n_1\times n_2}$ of reasonable complexity which approximates these data, i.e. such that $f(x_k)$ is close to $y_k$ for all $k\in [1, N]$ in the sense of certain criteria (root-mean-square error, maximum local error...). Remark: The case where an analytical expression $f_A:\mathbb{R}^n\rightarrow\mathbb{R}^{n_1\times n_2}$ is available instead of $N$ samples $\left\{(x_k, y_k),k\in [1, N]\right\}$ is not considered here (see e.g. [10]). Moreover, this library only deals with approximation (or regression) and not with interpolation, which would aim at finding a rational function $f$ such that the equalities $f(x_k)=y_k$ are strictly satisfied for a large number $N$ of samples (see [11] and references therein). The most common approach consists in restricting $f$ to be a polynomial function, that is: $$f(x)=P(x)=\sum_{i=0}^{n_P}a_ir_i(x)$$ where $\left\{r_i,i\in [1,n_P]\right\}$ is a set of polynomial regressors and $\left\{a_i,i\in [1,n_P]\right\}$ are coefficients to be determined.
- A classical solution is to solve a linear least-squares problem with respect to the coefficients $\left\{a_i,i\in [1,n_P]\right\}$, i.e. to minimize the following criterion [1]: $$C=\sum_{k=1}^{N}\left[y_k-P(x_k)\right]^2$$ This technique is implemented in the routine
lsapprox. - A well-known improvement to this approach relies on a preliminary orthogonalization process to decouple the regressors. As a result, the ability of each new regressor to reduce the criterion $C$ can be evaluated regardless of those already selected. Hence, only the most relevant ones can be considered, which amounts to a certain extent to minimizing the complexity of the polynomial approximation while still guaranteeing a low approximation error. This method was successfully applied by [7]. It was later improved, allowing to compute a sparse polynomial approximant satisfying the following global and local constraints: $$\left\{\begin{array}{ll}\sqrt{C/N}\le\epsilon_1\\|y_k-P(x_k)|\le\epsilon_2\ \ \ \forall k\in [1,N]\end{array}\right.$$ where $\epsilon_1$ and $\epsilon_2$ are some user-defined integers [4,5,6]. This orthogonal least-squares based variant is implemented in the routine
olsapprox.
$$f(x)=\frac{P(x)}{Q(x)}=\sum_{i=0}^{n_P}a_ir_i^P(x) \bigg/ \sum_{i=0}^{n_Q}b_ir_i^Q(x)$$ where $\left\{r_i^P,i\in [1,n_P]\right\}$ and $\left\{r_i^Q,i\in [1,n_Q]\right\}$ are two sets of polynomial regressors, while $\left\{a_i,i\in [1,n_P]\right\}$ and $\left\{b_i,i\in [1,n_Q]\right\}$ are coefficients to be determined.
- A first method consists in solving a nonlinear least-squares problem with respect to the coefficients $\left\{a_i,i\in [1,n_P]\right\}$ and $\left\{b_i,i\in [1,n_Q]\right\}$, that is to minimize the following criterion: $$C=\sum_{k=1}^{N}\left[y_k-\frac{P(x_k)}{Q(x_k)}\right]^2$$ It is notably implemented in the Curve Fitting toolbox of Matlab [2], where several optimization tools can be used to compute a solution (Levenberg-Marquardt algorithms, trust-region methods...). One of its major drawbacks is that several local minima may exist due to the non-convexity. Hence, the results strongly depend on the initialization, which is not a trivial issue. This approach is already available in Matlab and thus it is not implemented in this library.
- A second method was introduced by [12] in the context of polynomial approximation and then generalized by [3] to the rational case. Firstly, an uncertainty interval $\left[\underline{y}_k,\overline{y}_k\right]$ is defined around each $y_k$. A rational function is then determined which intersects all these intervals, i.e. $\underline{y}_k\le P(x_k)/Q(x_k)\le\overline{y}_k\ \forall k\in [1,N]$. This can be achieved by solving a Quadratic Programming problem in the coefficients $\left\{a_i,i\in [1,n_P]\right\}$ and $\left\{b_i,i\in [1,n_Q]\right\}$ with a strictly convex objective function. This algorithm is implemented in the routine
qpapprox.
These two algorithms suffer from the same drawback: all admissible monomials of $P$ and $Q$ are usually nonzero, regardless of their real ability to model the data. In this context, two additional methods have recently been developed to generate sparse rational approximations, which avoid data overfitting and lead to simple yet accurate LFR.
- A third method described in [8] looks for a rational approximation in a single step thanks to a symbolic regression technique. Genetic Programming is implemented to select sparse monomials and coupled with a nonlinear iterative procedure to estimate the coefficients of the resulting rational functions. The resulting algorithm is implemented in the routine
tracker. - A fourth method proposed in [9] performs the data approximation by building a sparse modeling based on neural networks, before translating the result into a fractional form. A stepwise selection algorithm is used, combining the benefits of forward orthogonal least squares to estimate the regression parameters, and of Particle Swarm Optimization to determine the best location of the regressors. The resulting algorithm is implemented in the routine
koala.
These two techniques usually compare very favorably to classical ones, as demonstrated on a realistic aeronautical example. For a given precision, the symbolic expressions are indeed more compact, and hence the size of the resulting LFR is smaller. Good numerical properties are also observed. Remark: It is usually desirable that the denominator of $f$ has no roots in the considered parametric domain, so as to ensure that $f$ has a smooth behaviour and that well-posed LFR are obtained. The algorithm implemented in koala always generates rational functions with strictly positive denominators. This is not true for the algorithms implemented in qpapprox and tracker, but in these two cases, a $\mu$-analysis based technique is implemented to check the nonsingularity of the resulting functions, and additional constraints are introduced until strictly positive denominators are obtained [8].
References
| [1] | J-F. Magni, Linear Fractional Representation toolbox for use with Matlab, available at http://w3.onera.fr/smac/, 2006. |
| [2] | The Mathworks, Curve fitting toolbox user's guide, 2010. |
| [3] | O.S. Celis, A. Cuyt and B. Verdonk, "Rational approximation of vertical segments", Numerical Algorithms, vol. 45, no. 1-4, pp. 375-388, 2007. |
| [4] | C. Poussot-Vassal and C. Roos, "Generation of a reduced-order LPV/LFT model from a set of large-scale MIMO LTI flexible aircraft models", Control Engineering Practice, vol. 20, no. 9, pp.919-930, 2012. |
| [5] | C. Roos, "Generation of flexible aircraft LFT models for robustness analysis", in Proceedings of the 6th IFAC Symposium on Robust Control Design, Haifa, Israel, June 2009. |
| [6] | C. Döll, C. Bérard, A. Knauf and J-M. Biannic, "LFT modelling of the 2-DOF longitudinal nonlinear aircraft behaviour", in Proceedings of the 9th IEEE Symposium on Computer-Aided Control System Design, San Antonio, Texas, September 2008, pp. 864-869. |
| [7] | E.A. Morelli and R. DeLoach, "Wind tunnel database development using modern experiment design and multivariate orthogonal functions", in Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, January 2003. |
| [8] | G. Hardier, C. Roos and C. Seren, "Creating sparse rational approximations for linear fractional representations using genetic programming", in Proceedings of the 3rd IFAC International Conference on Intelligent Control and Automation Science, Chengdu, China, September 2013, pp. 232-237. |
| [9] | G. Hardier, C. Roos and C. Seren, "Creating sparse rational approximations for linear fractional representations using surrogate modeling", in Proceedings of the 3rd IFAC International Conference on Intelligent Control and Automation Science, Chengdu, China, September 2013, pp. 238-243. |
| [10] | P.P. Petrushev and V.A. Popov, "Rational approximation of real functions", Encyclopedia of Mathematics and its Applications, vol. 28, University Press, Cambridge, 1987. |
| [11] | M.S. Floater and K. Hormann, "Barycentric rational interpolation with no poles and high rates of approximation", Numerische Mathematik, vol. 107, no. 2, pp. 315-331, 2007. |
| [12] | S. Markov, E. Popova, U. Schneider and J. Schulze, "On linear interpolation under interval data", Mathematics and Computers in Simulation, vol. 42, pp. 35-45, 1996. |