Please report any problems to Fabrice Demourant (fabrice.demourant@onera.fr). I will try to fix them as quickly as possible!
Overview
The IQC technique, which appeared during the nineties at least in its "modern form" [1], can be viewed as the merging of two well-known robustness analysis techniques, namely the (scaled) small gain techniques, the best known being $\mu$ analysis [2], and the positivity/passivity techniques which study the interconnection of an linear time invariant (LTI) operator with a non-linearity (the famous "Lur'e problem"). As a consequence, the IQC technique enables to study a wide range of problems, namely the robust stability and performance properties of the interconnection $M(s)-\Delta$ of an LTI operator M(s) with a structured model uncertainty $\Delta$ containing non-linearities, LTI and/or linear time-varying (LTV) parameters, neglected dynamics, delays, specific non-linearities such as friction or hysteresis... The principle is to replace each block of $\Delta$ by an IQC description of its inputs/outputs, i.e. the inputs/outputs of the block (e.g. a non linearity inside a sector, possibly with a bound on its slope) are supposed to satisfy a set of Integral Quadratic Constraints [1,3]. The finer the IQC description of the block, the less conservative the result. This approach is very interesting for two reasons. It includes in the same formalism a large set of linear and non linear stability theorems. Consequently the formalism used in the IQC approach can be described as an unified formalism. And secondly this unified formalism is based on inputs/outputs approach, namely a frequency domain approach, which makes it very attractive for high dimensional systems [6].
Principles and stability theorem
An IQC (Integral Quadratic Constraint) describes a relation between inputs and outputs signals of an operator. These constraints can be defined in the time or frequency domain since these two formulations are completely equivalent. Nevertheless frequency domain constraints are more often used, which leads to obtain stability conditions which are easier to handle. The definition of an IQC is given in the frequency domain: Two signals respectively of dimension $m$ and $p$, square integrable on $[0,\infty[$ i.e. : $$v \in L^m_2[0,\infty[ \; , \;\;\;\; w \in L^p_2[0,\infty[$$ satisfy the IQC defined by $\Pi$ if and only if \begin{equation} \int_{-\infty}^\infty \left[\begin{array}{c} \hat{v}(j \omega) \\ \hat{w}(j \omega)\end{array} \right]^* \Pi(j\omega) \left[\begin{array}{c}\hat{v}(j \omega) \\ \hat{w}(j\omega)\end{array}\right] d\omega \geq 0 \end{equation} where $\hat{v}(j \omega)$ and $\hat{w}(j \omega)$ respectively correspond to Fourier transforms of $v$ and $w$ such as $w=\Delta v$. A priori the operator $\Pi$, called multiplier, defined from $jR$ in $C^{(m+p)\times(m+p)}$ can be any measurable Hermitian-valued function. In most situations it is sufficient to use rational operators that are bounded on the imaginary axis.
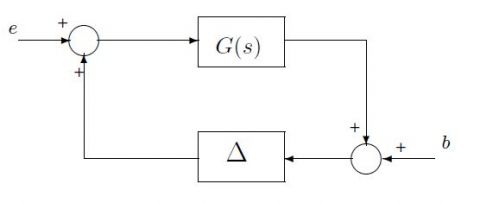
The problem consists in analyzing the closed loop of Figure 1 with $\Delta$ which can be non-linear and non-stationary. Let us suppose that inputs and output signals of $\Delta$ satisfy the IQC defined by $\Pi$. The following result gives the stability criterion [1]. Let us suppose $G(s)$ stable and $\Delta$ a causal and bounded operator:
- the interconnection of $G$ and $\tau \Delta$ is well posed for any $\tau \in [0,1]$,
- $\tau \Delta$ satisfies the IQCs defined by $\Pi$, $\forall\tau \in [0,1]$,
- it exists $\epsilon > 0$ such as: \begin{equation} \forall \omega \in R\quad \left[\begin{array}{c} G(j \omega) \\ I\end{array}\right]^* \Pi (j \omega) \left[\begin{array}{c} G(j \omega)\quad (1) \\ I\end{array}\right] \leq -\epsilon I\quad (1) \end{equation}
the closed loop system of the figure 1 is stable. It is important to notice that if $\tau\Delta$ satisfies several IQC $\Pi_1,\ldots,\Pi_n$, then a sufficient condition for the stability is that it exists $x_1,\ldots,x_n\geq 0$ such as the inequality 1 is satisfied for $\Pi=x_1\Pi_1+\ldots+x_n\Pi_n$.
A new algorithmic approach
In the context of this toolbox, we use standard IQC descriptions of the uncertainties and focus on the algorithmic issue. Let us remind that the stability criterion of this approach is based on frequency dependent inequalities (FDI). Then the most classical way to solve an IQC analysis problem consists in solving the state-space LMI conditions derived from the KYP lemma, so that the optimization variables come from the IQC multipliers, but also from an auxiliary matrix $P$. However, this solution becomes untractable when the order $n$ of the state-space representation becomes too high, since the number of scalar optimization variables in $P$ grows quadratically with $n$. Noting moreover that the initial state-space representation of M(s) is augmented with the state-space representations of the dynamic multipliers, so that even if the order of the initial state-space representation is low, it may increase very fast when introducing dynamic multipliers. Different approaches based on Hamiltonian matrix as been developed ([4] for example and references therein) to avoid this problem. Here an alternative technique is implemented. The approach developed here is particularly attractive due to its conceptual simplicity. Besides the technique is based on very usual and common solver which is the LMI/Robust control Toolbox of Matlab. In brief the implementation is straightforward, completely self-contained in Matlab environment, which might useful for engineers in need for efficient and fast answers to analyze stability of complex problems.
To involve the frequency domain resolution a specific approach which consists in checking the validity of the solution on the whole frequency domain has been developed. This approach is based on a mathematical result on the singular value maximum of an LFT (Linear Fractional Transformation) structure where the $\Delta_r$ block is a real perturbation model [6,7]. More precisely when a solution is obtained from a frequency domain griding the stability criterion which depends on frequencies is put under an LFT form to make appear the frequency $\omega$ as a real parameter in the $\Delta_r$ block of the LFT. It is important to notice that this $\Delta_r$ block is completely different from the $\Delta$ block of the closed loop to analyze (see figure 1). In our context $\Delta_r$ contains $\omega$ and is obtained from an LFT representation of the stability criterion (1).
Then the validity domain of the solution is computed thanks to an algebraic approach extracted from [5] and adapted to our problem [6,7]. For a non-rational description of multipliers the method has been extended in [8,9]. The non-rational representation is not yet implemented in the toolbox. If this domain is $[0, +\infty[$ the solution is valid on the whole frequency domain. Else, frequencies where the FDI are not satisfied are detected and are added to the initial frequency domain griding and a new solution is computed with the new griding and so on. If no solution is obtained on the griding the problem is considered as unfeasible. In brief the stability problem is recast as an LMI feasibility problem where the constraints (FDI) are added iteratively. Finally the number of optimization variables is completely independent of the model order.
References
| [1] | A. Megretski and A. Rantzer, "System analysis via Integral Quadratic Constraints", in IEEE Transactions on Automatic Control, vol. 42, no. 6, pp. 819-829, 1997. |
| [2] | M.K.H Fan, A.L. Tits and J.C. Doyle, "Robustness in the presence of mixed parametric uncertainty and unmodeled dynamics", IEEE Transactions on Automatic Control, vol. 36, no. 1, pp. 25-38, 1991. |
| [3] | U.T. Jonsson, Lecture notes on integral quadratic constraints, 2001. |
| [4] | C. Kao, A. Megretski, and U.T. Jönsson, Specialized fast algorithms for IQC feasibility and optimization problems, Automatica, vol. 40, no. 2, pp. 239-252, 2004. |
| [5] | A. Sideris, and R.S. Sanchez Pena, "Robustness margin calculation with dynamic and real parametric uncertainty", IEEE Transactions on Automatic Control, vol. 35, no. 8, pp. 970 -974, 1990. |
| [6] | F. Demourant, T.P. Vo Hoang, and A. Pavie "Analysis of the aeroelastic stability with freeplay in a control surface by integral quadratic constraints approach", International Forum on Aeroelasticity and Structural Dynamic (IFASD), 2011. |
| [7] | F. Demourant, "New algorithmic approach based on integral quadratic constraints for stability analysis of high order models", Control Conference (ECC), 2013 European, pp. 359-364, 2013. |
| [8] | P. Vuillemin, F. Demourant, J-M. Biannic, and C. Poussot-Vassal, "Global stability validation of an uncertain large-scale aircraft model", Control Applications (CCA), 2014 IEEE Conference on , pp. 152-157, 2014. |
| [9] | P. Vuillemin, F. Demourant, J-M. Biannic, and C. Poussot-Vassal, "Stability Analysis of a Set of Uncertain Large-Scale Dynamical Models With Saturations: Application to an Aircraft System", IEEE Transactions on Control Systems Technology, vol. PP, no. 99, pp. 1-8, 2016, DOI: 10.1109/TCST.2016.2558542. IEEE Early Access. |