A simple example to illustrate the use of the GSS library

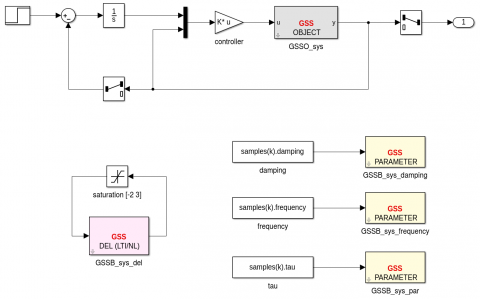
This simple example shows how the GSS library with the GSSLIB Simulink interface can be used to design a controller for a nonlinear uncertain system and to perform a basic robustness analysis.

Problem statement

The considered open-loop plant is the series interconnection of:

  • a 1st order actuator with uncertain time constant and position limits,
  • a 2nd order system with uncertain frequency and damping.

\begin{equation} \left\{\begin{array}{ccl}\dot{x_1}&=&-\color{darkgreen}{\tau} x+u\\[4pt]v&=&\color{red}{\textrm{sat}_{[-2,3]}(}x_1\color{red}{)}\\[4pt]\color{darkgreen}{\tau}&\color{darkgreen}{\in}&\color{darkgreen}{[\begin{array}{cc}0.08&0.12\end{array}]}\end{array}\right. \hspace{3cm} \left\{\begin{array}{ccl}\ddot{x_2}&=&-2\color{orange}{\xi\omega}\dot{x_2}-\color{orange}{\omega^2}x_2+\color{orange}{\omega^2}v\\[4pt]y&=&\left[\begin{array}{cc}x_2&\dot{x_2}\end{array}\right]^T\\[4pt]\color{orange}{\omega}&\color{orange}{\in}&\color{orange}{[\begin{array}{cc}1&3\end{array}]}\\[4pt]\color{orange}{\xi}&\color{orange}{\in}&\color{orange}{[\begin{array}{cc}0.1&0.5\end{array}]}\end{array}\right. \end{equation} The objective is to design a PID controller such that the uncertain closed-loop plant behaves like a second-order system with frequency > 1 rad/s and damping > 0.7.

The objective is to design a PID controller such that the uncertain closed-loop plant behaves like a second-order system with frequency > 1 rad/s and damping > 0.7.

Creation of the open-loop GSS object

The actuator with uncertain time constant and position limits is modeled first: 

>> sat=gss('position','SAT',[1 1],1,[-2 3]);
>> tau=gss('tau',0.1,[0.08 0.12]);
>> actuator=sat*tf(1,[tau 1]);
>> size(actuator) 

Warning: Normalization has been performed to avoid inversion problems.

Continuous-time GSS object actuator with 1 output, 1 input and 1 state.
2 blocks in Delta: global size = 2x2.
Name      Type        Size    Measured  NomValue    Bounds
position  SAT         1x1     ?         1           limits = [-2 3]
tau       PAR (real)  1x1     no        0           min/max = [-1 1]

The second-order system with uncertain frequency and damping is defined next. First solution: the state-space matrices are defined as gss objects. 
>> xi=gss('damping',0.3,[0.1 0.5]);
>> omega=gss('frequency',2,[1 3]);
>> A=[0 1;-omega^2 -2*xi*omega];
>> B=[0;omega^2];
>> C=[1 0;0 1];
>> D=[0;0];

They are turned into a dynamic model. 

>> setred('no')
>> sys1=ss(A,B,C,D);
>> size(sys1)

Continuous-time GSS object sys1 with 2 outputs, 1 input and 2 states.
2 blocks in Delta: global size = 6x6.
Name       Type       Size  Measured  NomValue  Bounds
damping    PAR (real) 1x1   no        0.3       min/max = [0.1 0.5]
frequency  PAR (real) 5x5   no        2         min/max = [1 3] 

$\Rightarrow$ frequency is repeated 5 times if no order reduction is performed. 

>> setred('default')
>> sys1=ss(A,B,C,D);
>> size(sys1)

Continuous-time GSS object sys1 with 2 outputs, 1 input and 2 states.
2 blocks in Delta: global size = 4x4.
Name       Type       Size  Measured  NomValue  Bounds
damping    PAR (real) 1x1   no        0.3       min/max = [0.1 0.5]
frequency  PAR (real) 3x3   no        2         min/max = [1 3]          

$\Rightarrow$ frequency is repeated 3 times if order reduction is performed. 

Second solution: The state-space matrices are defined as symbolic objects. 

>> syms frequency damping
>> A=[0 1;-frequency^2 -2*damping*frequency];
>> B=[0;frequency^2];
>> C=[1 0;0 1];
>> D=[0;0];

They are turned into a dynamic model. 

>> abcd=sym2gss([A B;C D]);
>> sys2=abcd2gss(abcd,2);
>> set(sys2,'damping','NomValue',0.3,'Bounds',[0.1 0.5]);
>> set(sys2,'frequency','NomValue',2,'Bounds',[1 3]);
>> size(sys2)

Continuous-time GSS object sys2 with 2 outputs, 1 input and 2 states.
2 blocks in Delta: global size = 3x3.
Name       Type       Size  Measured  NomValue  Bounds
damping    PAR (real) 1x1   no        0.3       min/max = [0.1 0.5]
frequency  PAR (real) 2x2   no        2         min/max = [1 3]

$\Rightarrow$ frequency is repeated twice, which corresponds to the minimal realization.

It can be checked that the two gss objects are equivalent. 

>> distgss(sys1,sys2)

$\Rightarrow$ the returned value is zero!

The gss object sys2 is simpler and is thus considered in the sequel. 

>> sys=sys2;

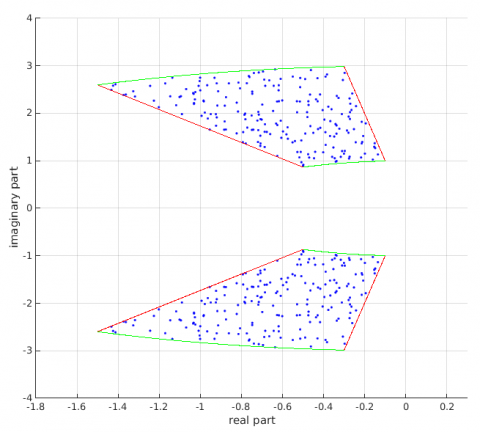
The linearized open-loop plant is analyzed. The saturation is ignored and 200 random samples are computed. 

>> sys_lin=eval(sys,'position','nominal');
>> [sys0,samples]=dbsample(sys_lin,200);
>> figure,hold on,grid on
>> for k=1:length(sys0)
>>     ev=eig(sys0{k});
>>     plot(real(ev),imag(ev),'b.')
>> end
>> xlim([-1.8 0.3]);
>> ylim([-4 4]);
>> plot(-0.1*[1 3],sqrt(1-0.1^2)*[1 3],'r-')
>> plot(-0.1*[1 3],-sqrt(1-0.1^2)*[1 3],'r-')
>> plot(-0.5*[1 3],sqrt(1-0.5^2)*[1 3],'r-')
>> plot(-0.5*[1 3],-sqrt(1-0.5^2)*[1 3],'r-')
>> theta=1.671:0.001:2.095;
>> plot(cos(theta),sin(theta),'g-')
>> plot(3*cos(theta),3*sin(theta),'g-')
>> plot(cos(-theta),sin(-theta),'g-')
>> plot(3*cos(-theta),3*sin(-theta),'g-')
>> xlabel('real part')
>> ylabel('imaginary part')

open_loop_poles
 Figure 1: Open-loop poles obtained with 200 random samples

 

The damping ratio and the frequency lie between the considered bounds in all cases.

The actuator and the 2nd order system are finally connected. 

>> sys=sys*actuator;
>> size(sys)

Continuous-time GSS object sys with 2 outputs, 1 input and 3 states.
4 blocks in Delta: global size = 5x5.
Name       Type        Size  Measured  NomValue  Bounds
position   SAT         1x1   ?         1         limits = [-2 3]
damping    PAR (real)  1x1   no        0.3       min/max = [0.1 0.5]
frequency  PAR (real)  2x2   no        2         min/max = [1 3]
tau        PAR (real)  1x1   no        0         min/max = [-1 1]

PID controller design

A PID controller is now designed using pole placement.

closed_loop_nude
Figure 2: Closed-loop interconnection

 

The objective is to design the 1$\times$3 static matrix gain $K$ so that the uncertain closed-loop plant sys behaves like a second-order system with frequency > 1 rad/s and damping > 0.7.

An augmented open-loop plant including an integrator is first computed.

Direct computation 

>> Int=gss('Int');
>> sysaug1=[-Int 0;1 0;0 1]*sys;

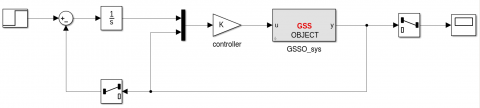
Use of the Simulink library GSSLIB

open_loop_for_design
 Figure 2: Open-loop design model created with GSSLIB

 

>> sysaug2=slk2gss('open_loop_plant');

Comparison 

>> distgss(sysaug1,sysaug2)

          $\Rightarrow$ the returned value is zero! 

>> sysaug=sysaug1;

 An LTI model corresponding to the lowest damping ratio and the lowest frequency is considered for design. 

>> syslti=eval(sysaug,{'position' 'tau' 'damping' 'frequency'},{'nominal' 'nominal' 0.1 1});
>> damp(syslti)

An eigenstructure assignment algorithm is applied. The main objective is to improve the damping factor, which is set to 0.8. 

>> xi_target=0.8;
>> omega_target=2;
>> lambda=[roots([1 2*xi_target*omega_target omega_target^2]);-2*omega_target];
>> for k=1:3
>>     vw(:,k)=null([syslti.a-lambda(k)*eye(4) syslti.b]);
>> end
>> K=real(vw(5,:)*inv(syslti.c*vw(1:4,:)));
>> damp(syslti.a+syslti.b*K*syslti.c)
        Pole            Damping     Frequency    Time Constant -4.00e+00               1.00e+00     4.00e+00       2.50e-01
-3.00e+00               1.00e+00     3.00e+00       3.33e-01
-1.60e+00 + 1.20e+00i   8.00e-01     2.00e+00       6.25e-01
-1.60e+00 - 1.20e+00i   8.00e-01     2.00e+00       6.25e-01

The static controller $K=[\begin{array}{ccc}4.80&-5.64&-3.54\end{array}]$ is obtained.

The open-loop model and the controller are interconnected to get the closed-loop plant.

>> syscl=feedback(sysaug,K,[],[],1);

Note that it can also be done using the Simulink library GSSLIB.

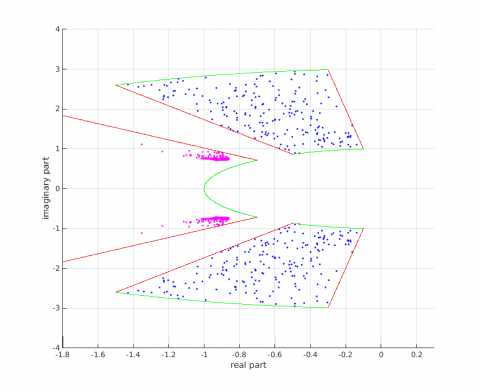
The linearized closed-loop plant is analyzed. The saturation is ignored and 200 random samples are computed. 

>> syscl_lin=eval(syscl,'position','nominal');
>> [sys0,samples]=dbsample(syscl_lin,200);
>> syscl_lin=eval(syscl,'position','nominal');
>> [sys0,samples]=dbsample(syscl_lin,200);
>> for k=1:length(sys0)
>>     ev=eig(sys0{k});
>>     plot(real(ev),imag(ev),'m.')
>> end
>> plot(-0.7*[1 3],sqrt(1-0.7^2)*[1 3],'r-')
>> plot(-0.7*[1 3],-sqrt(1-0.7^2)*[1 3],'r-')
>> theta=pi-0.795:0.001:pi+0.795;
>> plot(cos(theta),sin(theta),'g-')

closed_loop_poles
Figure 4: Closed-loop poles (pink) and open-loop poles (blue) obtained with 200 random samples

The damping ratio and the frequency lie inside the considered bounds in all cases.

Closed-loop analysis

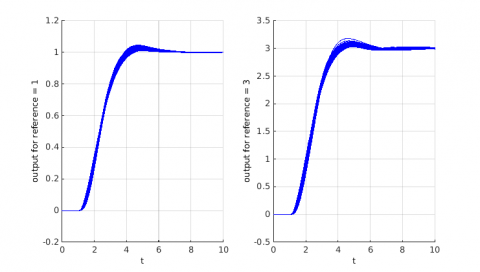
The nonlinear closed-loop plant is analyzed. A simulation is performed (including the saturation) for each of the 200 random samples computed previously.

closed_loop_for_validation
Figure 5: Closed-loop validation model created with GSSLIB

>> figure
>> subplot(1,2,1),hold on,grid on
>> ref=1;
>> for k=1:length(sys0)
>>     [t,x,y]=sim('closed_loop_plant_uncertain');
>>     plot(t,y,'b-');
>> end
>> xlabel('t')
>> ylabel('output for reference = 1')
>> subplot(1,2,2),hold on,grid on
>> ref=3;
>> for k=1:length(sys0)
>>     [t,x,y]=sim('closed_loop_plant_uncertain');
>>     plot(t,y,'b-');
>> end
>> xlabel('t')
>> ylabel('output for reference = 3')
>> subplot(1,3,3),hold on,grid on

closed_loop_simulations
 Figure 4: Closed-loop simulations for the 200 random samples

 

The closed-loop behavior is in accordance with the specifications, but the influence of the saturation can be seen for a reference input of 3.

It seems to work... but further validation is required. This can for example be achieved with other libraries of the SMAC Toolbox (SMART, SAW, IQC).