Routine koala

Rational approximation of tabulated data using surrogate modeling.

Description

This routine uses Surrogate Modeling to compute a multivariate rational approximation $f:\mathbb{R}^n\rightarrow\mathbb{R}^q$ of a set of samples $\left\{y_k\in\mathbb{R}^q, k\in [1, N]\right\}$ obtained for different values $\left\{x_k\in\mathbb{R}^n,k \in [1, N]\right\}$ of some explanatory variables $x$. The maximum degree of the rational function is set by the user and a factorized expression is obtained. Unless specified, its nonsingularity is guaranteed on the whole considered domain (defined as the convex hull of $\left\{x_k\in\mathbb{R}^n,k \in [1, N]\right\}$).

Beyond the polynomial/rational expressions, the use of surrogate models becomes widespread among many scientific domains to replace the system or the reference model when this one is too restrictive for achieving some tasks like optimization, modeling, parameter identification [1,6]... Hence, a wide range of methods has been developed for building surrogate models efficiently, i.e. with both accuracy and parsimony. For example, Neural Networks (NN) are recognized nowadays as an efficient alternative for representing complex nonlinear systems, and tools are available to model static nonlinearities such as the ones encountered when formulating a problem in LFR form. The underlying idea for solving the considered approximation problem via an indirect approach consists in using such methods to derive a rational model. The tool used in the sequel was developed by ONERA for aircraft modeling and identification purposes and is named KOALA (Kernel Optimization Algorithm for Local Approximation). See [1,6,10] for more details.

KOALA algorithm in a few words

At first, it is noteworthy that a nonlinear model can be either linear, nonlinear, or both in regard to its internal parameters. For NNs, the latter case corresponds to multilayer perceptrons [7], but also to Radial Basis Function Networks (RBFN) when the centers and the radii of the radial units are optimized [5]. However, the joint optimization of the whole set of model parameters (linear and nonlinear) practically results in ill-posed problems, and consequently in convergence and regularization issues. That is why Linear-in-their-Parameters models (LP) are often adopted, allowing simpler and more robust algorithms to be developed. By taking advantage of their features, structural identification, i.e. determining the best set of regressors from the available data only, becomes possible in addition to parametric estimation.

To choose the unknown regressors, KOALA is based on forward selection, starting with an empty subset and adding them one at a time in order to gradually improve the approximation. To speed up that constructive process, a preliminary orthogonalization technique is used, permitting the individual regressors to be evaluated regardless of those previously recruited for the modeling [2]. In the case of local models like RBFN, choosing each regressor amounts to optimizing the kernel functions in the input space. To implement this optimization step, a global method is the best suited, and KOALA uses a new evolutionary metaheuristic known as Particle Swarm Optimization (PSO) [4]. The performance of this approach is strongly dependent on the algorithms added to the basic version of PSO (e.g., [3] uses a standard and very simple version of PSO). After a thorough literature analysis, the most promising techniques have been selected and implemented in the part of the KOALA code used to optimize the regressors' positioning (PSO internal library). A brief survey of its main functionalities is given below (see [10] and the references therein for more details):

fixed and adaptive topologies $\rightarrow$ from static (star, ring, Von Neumann) to dynamic ones (e.g. Delaunay neighboring)
particle's displacement $\rightarrow$ standard, with constriction factor, FIPS and weighted FIPS versions of the velocity update laws
hybrid local/global method $\rightarrow$ to speed up the convergence with direct search (improved Nelder-Mead, Delaunay tessellation for the initial simplex)
multiswarm strategies $\rightarrow$ for competing swarms or for partitioning the search domain into several subregions
diversity analysis $\rightarrow$ to provide information about the swarm dispersion and to refine the convergence tests
swarm initialization $\rightarrow$ from random to low-discrepancy sequences (Hammersley, centroidal Voronoï diagram)
competitive multirun $\rightarrow$ to benefit from several topologies, algorithm variants and tuning
charged vs neutral particles $\rightarrow$ cooperation of particles with different physical properties.

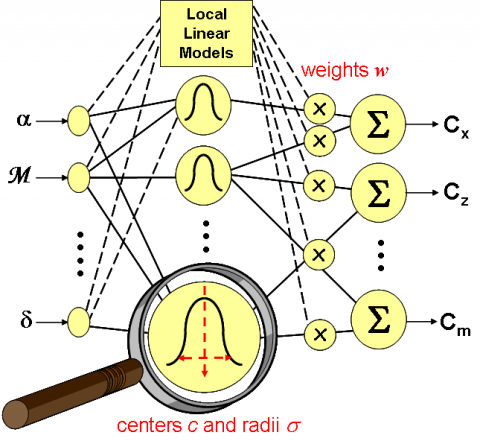
The coupling of that PSO algorithm with the constructive technique detailed in [10] allows to proceed to structural and parametric optimizations jointly for different types of regressors with local basis. In the case of KOALA, it is applied to RBFN but also to Local Linear Models (LLM) after some adjustments of the OLS method. LLM networks generalize RBFN, and gave rise to the famous LOLIMOT algorithm (LOcal LInear MOdel Tree) [9]. They are also related to other local models like Fuzzy Inference Systems. They are derived by replacing the RBF linear weightings (called singletons in the fuzzy community), and denoted by $w$ in the sequel, by an affine expression depending on the model inputs. It is thus expected that fewer kernels will be required to achieve the same accuracy in most applications. For LLM, the generic formulation used to represent LP models is (assuming a scalar function to simplify the notations):

$(1)\hspace{2cm}y_k=f(x_k)=\displaystyle\sum_{j=1}^m\bigg[\sum_{i=0}^nw_{ji}x_k^i\bigg]r_j(x_k)=\sum_{l=1}^{m(n+1)}w_l\ r_l^{\#}(x_k)$

where $r_j(x_k)$ represents the kernel value of the $j^{th}$ regressor function, and with $x_k^0=1$ to include the constant terms of the affine modeling into the second sum. This relationship permits to recover a standard LP formulation with an extended set of regressors $r_l^{\#}$. To adapt the constructive algorithms to the kernel functions $r_l^{\#}$, the group of regressors sharing the same kernel $r_j$ needs to be considered as a whole when adding or subtracting terms, and no more separately as it was the case for RBFN [2] or polynomials [8].

RBFN/LLM-type surrogate models optimized by KOALA

KOALA aims at gradually selecting a series of regressors by optimizing their kernel parameters, i.e. the ellipsoid centers $c$ and radii $\sigma$ related to the radial unit. At each step of the process, the PSO particles are associated with vectors of $\mathbb{R}^{2n}$ gathering these parameters for the $n$ explanatory variables. To sum up, the global performance of the KOALA algorithm results from two complementary aspects: applying efficient OLS-based forward selection and Separable Nonlinear Least Squares optimization to powerful modeling (LLM) and, on the other hand, implementing a new PSO algorithm which outperforms the standard ones [10]. To give a rough idea, the use of KOALA results in a model comprising only 5 radial units in the common benchmark case (for a global quadratic error $C=2.5\ 10^{-3}$), whereas a more standard algorithm, e.g. the one of [3], requires not less than 15 RBF units to achieve the same level of approximation. Hence, the (maximum) degree of the rational approximant can be reduced from 30 to 10 and the LFR size from 60 to 20.

Back to rational modeling, a first idea for an indirect approach capitalizing on KOALA results is to convert equation (1) a posteriori into a rational form. By choosing Gaussian radial functions, this regression expresses as the sum of $m$ terms, the $j^{th}$ one being for any $x$:

$(2)\hspace{2cm}f_j(x)=\bigg[\displaystyle\sum_{i=0}^nw_{ji}x^i\bigg]r_j(x)=\bigg[\sum_{i=0}^nw_{ji}x^i\bigg]\large{exp}^{-\displaystyle\sum_{i=1}^n(x^i-c_{ji})^2/\sigma_{ji}^2}$

Therefore, it is possible to use Pade approximants of the exponential function, so as to replace it by a rational function in reduced form $exp_{[p,q]}$. The latter expresses as the quotient of two polynomials of the $p^{th}$ and $q^{th}$ degrees, and the corresponding approximant to $f_j(x)$ becomes a rational function of the $(2p+1)^{th}$ and $2q^{th}$ degrees for every explanatory variable $x^i$. However, getting high quality approximants (e.g. decreasing rapidly to 0 as $x^i$ increases) requires large values for $q$ (with $q-p$ greater than 2 or 3). Hence, the degree of the resulting rational function is penalized, with no guarantee about the accuracy of the global regression $f(x)$ . On the other hand, a more relevant approach consists in replacing the exponential function straight away by such an approximant, and then to proceed to the optimization of the regression with this new kernel function. The simplest transform corresponds to the reduced form $exp_{[0,1]}$, i.e. to the sum of $m$ components like:

$(3)\hspace{2cm}f_j(x)=\bigg[\displaystyle\sum_{i=0}^nw_{ji}x^i\bigg]\bigg/\bigg[1+\sum_{i=1}^n(x^i-c_{ji})^2/\sigma_{ji}^2\bigg]$

Hence, another class of models was added to the RBF/LLM kernels proposed by KOALA, based on the Pade approximant $exp_{[0,1]}$. It must also be mentioned to conclude that the post-processing of the resulting regression, prior to the derivation of the LFR, makes use of the Matlab© Symbolic Toolbox. Again, several options can be considered for gathering the $m$ components $f_j(x)$ into a single rational function: global expansions of numerator and denominator, factorization of the denominator, sum of elementary rational terms. The latter appears to be the most relevant since it favors some simplifications when building the final LFR. A factor of two can usually be gained in the final LFR size.

Syntax

[fdata,fdesc,fsym,flfr,Vloo,CI]=koala(X,Y,names,{maxdeg,options})

Input arguments

The first three input arguments are mandatory and the fourth one is optional:

`X`	Values $\left\{x_k\in\mathbb{R}^n,k \in [1, N]\right\}$ of the explanatory variables $x$ ($n\times N$ array, where `X(:,k)` corresponds to $x_k$).
`Y`	Samples $\left\{y_k\in\mathbb{R}^{q}, k\in [1, N]\right\}$ to be approximated ($q\times N$ array where `Y(:,k)` corresponds to $y_k$.
`names`	Names of the explanatory variables $x$ ($1\times n$ cell array of strings).
`maxdeg`	Maximum degree of the approximating rational function $f$ (even integer, default=100). During optimization, `maxdeg/2` kernels are created unless the target value `options.target` is defined and reached with less kernels.

The fifth input argument is an optional structured variable. Default values are given between brackets. Most of the parameters can be left to their default setting, some of them (swarm topology, PSO parameters) being especially devoted to experienced users. The most important ones are target and rbf.

options

$\hspace{0.65cm}$General and modeling issues

weights: [ones(1,N)] vector containing the weighting coefficients applied to the data samples ; if $q>1$, it should remain a vector, and the weights are identically applied to the data samples for each output.
target: [0] minimum criterion value for stopping (choose 0 to run till degree maxdeg (if defined) or till 50 kernels at most).
rbf: [0] type of modeling involved in the local approximation:
- 0 = LLM (Local Linear Model)
- 1 = standard RBF network
type: [1] type of radial cell:
- 0 for Gaussian $[e^{-r^2}]$ (not available for LFR modeling)
- 1 for Pade order 1 $[1/(1+r^2)]$
- 2 for pseudo-Pade $[1/(1+|r|)]$ (not available for LFR modeling)
B: [] $n\times 4\times n_z$ array containing the lower/upper bounds associated to the kernel parameters ; the 3rd dimension is optional if the number $n_z$ of data zones (see options.nbzone) is 1 ; this matrix must be filled in by the user when the number $n_z$ of data zones is different from 1 ; the different bounds are splitted along the 2nd dimension as follows:
- B(:,1,:) for the lower bounds of the centers
- B(:,2,:) for the lower bounds of the radii
- B(:,3,:) for the upper bounds of the centers
- B(:,4,:) for the upper bounds of the radii
snls: [5] number of iterations between Separable Nonlinear Least Squares (SNLS) optimizations (Inf if no SNLS optimization, negative number to speed up the SNLS stages).
loo: [1] optimization based on a Leave-One-Out/Predicted Residual Sum of Squares (LOO/PRESS) generalization criterion (default) or on the usual sum of squares.
trace: [1] trace of execution (0=no, 1=text, 2=text+figures).
viewpoint: [0 0] deviation with respect to the default viewpoint (see plotapprox) ; applicable only if 3-D graphs are to be displayed (options.trace=2 and $n=2$).
Convergence parameters w.r.t. PSO algorithm
maxit: [200] maximum number of PSO iterations.
cvgce1: [0.05] relative variation of criterion (%).
cvgce2: [5] normalized average speed of swarm particles (%).
nbstep2stop: [4] number of successive steps required for satisfying the stopping criteria.
Topology of the swarms
nbswarm: [1] number of swarms competing for the best result or acting in several sub-domains.
nbzone: [1] number of optimization sub-domains $n_z$.
nbtrial: [1] number of PSO strategies/topologies to be run successively in case of failure.
nbpart: [16] number of particles in each swarm.
charged: [0] creating charged particles in each swarm in addition to the usual neutral ones.
Processing the best result of each PSO iteration
mutation: [0] mutation process of the (global) best particle (especially useful for multimodal problems).
stdmax: [0.5] standard max bound for the normal distribution of the mutation process.
stdmin: [0.5] standard min bound for the normal distribution of the mutation process.
local: [1] local optimization to improve the (global) best particle.
delaunay: [0] Delaunay tessellation for computing best neighbors (dynamic topologies).
neldermead: [0] local optimization using Nelder-Mead algorithm in addition.
Cross-validation and confidence intervals
Xv: [] $n\times M$ array containing the values of the explanatory variables used for cross-validation ($M$ samples).
Yv: [] $q\times M$ array containing the samples used for cross-validation ($M$ samples).
Xci: [] $n\times P$ array containing the values of the explanatory variables used to compute the confidence intervals ($P$ samples).

Output arguments

`fdata`	Values $\left\{f(x_k)\in\mathbb{R}^q,k \in [1, N]\right\}$ of the approximating function $f$ (same size as `Y`).
`fdesc`	Structured variable describing the approximating function $f$: `nbker`: number of kernels (radial units) involved in the final model. `centers`: $n \times nbker$ array containing the components of the $nbker$ kernel centers. `radii`: $n \times nbker$ array containing the components of the $nbker$ kernel radii. `teta`: $nbker \times nbw$ array containing the regression parameters in the user model space, with $nbw=1$ for standard RBF networks (`options.rbf=1`) or $nbw=n+1$ for Local Linear Models (`options.rbf=0`).
`fsym`	Symbolic representation of the approximating function $f$ (symbolic object).
`flfr`	Linear fractional representation of the approximating function $f$ (GSS object if the GSS library is installed, LFR object otherwise if the LFR toolbox is installed). Even if this cannot be proved, its size is usually equal to $n$`*maxdeg`.
`Vloo`	Variance of the outputs (Leave-One-Out type) computed on the estimation data X ($q\times N$ array). Remark: The absolute value of the LOO-type variance is mainly useful for designing adaptive DoE (Design of Experiments). However, the relative value get for the different samples can be used for comparing the data samples and for displaying the regions with poor data sampling w.r.t. the function non-linearities (see the examples below).
`CI`	Confidence Interval (99%) of the outputs computed on the data `Xci` ($q\times P$ array). Remark: Practically, the value of the confidence intervals depends on the estimated value of the prediction error variance which is generally under-estimated by the algorithm. As for `Vloo` variances, relative comparisons are relevant. Otherwise, confidence intervals can be computed anywhere in the domain inside or outside the data convex hull to detect "hidden" extrapolations or bad interpolation areas.

Example

Drag coefficient of a generic fighter aircraft model:

load data_cx
% (X1,Y1) => first grid for approximation with 1196 scalar samples
% (X2,Y2) => second grid for approximation with 2501 scalar samples
% (X2,Y2x2) => second grid for approximation with 2501 2x1 samples
% (X3,Y3) => third grid for approximation with 504 scalar samples
% (Xv,Yv) => grid for validation with 4641 scalar samples
%(Xv,Yvx2) => grid for validation with 4641 2x1 samples

% alfa angle converted from radians to degrees (estimation and validation data)
X2(2,:)=X2(2,:)*57.3;
X3(2,:)=X3(2,:)*57.3;
Xv(2,:)=Xv(2,:)*57.3;

Run #1: rough approximation of the 8th degree

% approximation on a rough grid with koala
maxdeg=8; % degree of the rational approximation (creates maxdeg/2 kernels)
clear koala_options
koala_options.rbf=0; % LLM type (Local Linear Model)
koala_options.snls=-3; % nb of iterations between SNLS stages (negative to speed up SNLS)
[fdata,fdesc,fsym,flfr,Vloo,CI]=koala(X2,Y2,names,maxdeg,koala_options);

Size of the LFR: (trial#1 --> 16/ trial#2 --> 16) ==> Minimum size = 16
Symbolic expression of the rational approximation:
(0.0405329+0.104062*Ma-0.00366468*Al)/(3.56902+2.77849*Ma^2-2.43896*Ma+0.0028391*Al^2-0.151975*Al)
+(-0.119834+0.0191823*Ma+0.00218966*Al)/(10.864+18.5162*Ma^2-22.9496*Ma+0.00295651*Al^2-0.180431*Al)
+(0.0260956-0.00899047*Ma-0.00430757*Al)/(4.43738+2.77778*Ma^2-1.72953*Ma+0.0188308*Al^2-0.488504*Al)
+(0.0353674-0.0387467*Ma-0.000263254*Al)/(4.46828+3.53044*Ma^2-6.9872*Ma+0.530133*Al^2+0.153685*Al)

% compute estimation errors on a rough grid
eps=Y2-fdata; sse=eps*eps'; std=sqrt(sse/length(eps)); [maxerr,kmax]=max(abs(eps));
fprintf('Estimation errors : Global=%e - RMS=%e - Max local=%e\n',sse,std,maxerr);
% plot 3D surfaces and compute validation errors on a fine grid plosurfaces(fsym,X2,Y2,names,Xv,Yv,Vloo,CI);

Estimation errors : Global=1.611133e-003 - RMS=8.026180e-004 - Max local=5.369329e-003
Validation errors : Global=2.917519e-003 - RMS=7.928683e-004 - Max local=5.369967e-003

Approximation and validation results (LLM model/degree 8)

Run #2: fine approximation of the 16th degree

% approximation on a rough grid with koala
maxdeg=16; % degree of the rational approximation (creates maxdeg/2 kernels)
clear koala_options
koala_options.rbf=0; % LLM type (Local Linear Model)
koala_options.snls=-3; % nb of iterations between SNLS stages (negative to speed up SNLS)
koala_options.nbswarm = 3; % nb of swarms competing for the best result (to illustrate the use of this optional parameter, but the same accuracy would be got with only 1 swarm here)
[fdata,fdesc,fsym,flfr,Vloo,CI]=koala(X2,Y2,names,maxdeg,koala_options);

Size of the LFR: (trial#1 --> 32/ trial#2 --> 32) ==> Minimum size = 32
Symbolic expression of the rational approximation:
(0.13446+8.65439e-005*Ma-0.0112829*Al)/(1.97326+2.77983*Ma^2-1.5889*Ma+0.00945984*Al^2-0.168036*Al)
+(-0.256991-0.113071*Ma+0.00257907*Al)/(3.34466+3.8883*Ma^2-4.7306*Ma+0.00103735*Al^2-0.0613074*Al)
+(0.18544+0.270942*Ma-0.00467659*Al)/(3.04052+2.77787*Ma^2-3.11751*Ma+0.00128546*Al^2-0.0774248*Al)
+(0.0101332-0.0054054*Ma-0.000929947*Al)/(1.55897+2.77778*Ma^2-2.4921*Ma+0.410102*Al^2-0.00616852*Al)
+(-0.00757304+0.00479486*Ma-7.42993e-005*Al)/(107.053+2.77778*Ma^2-2.6114*Ma+0.467042*Al^2-14.0349*Al)
+(-0.0140033+0.00902958*Ma+4.98902e-005*Al)/(117.13+315.509*Ma^2-379.744*Ma+0.00232742*Al^2-0.131788*Al)
+(-0.0906197+0.00499768*Ma+0.00643751*Al)/(1.89044+4.59244*Ma^2-2.58843*Ma+0.00890246*Al^2-0.136823*Al)
+(0.0341298-0.0555376*Ma-9.42095e-005*Al)/(6.24781+7.38814*Ma^2-12.4534*Ma+0.00618907*Al^2+0.000356309*Al)

Estimation errors : Global=1.622899e-004 - RMS=2.547352e-004 - Max local=1.407199e-003
Validation errors : Global=3.459735e-004 - RMS=2.730333e-004 - Max local=1.407783e-003

Approximation and validation results (LLM model/degree 16)

Run #3: fine approximation with RBF-type model

% approximation on a rough grid with koala
clear koala_options
koala_options.target = 2e-7; % target value for the error of the rational approximation (about the same as previous run #2)
koala_options.rbf=1; % RBF type (standard Radial Basis Function network)
koala_options.snls=-3; % nb of iterations between SNLS stages (negative to speed up SNLS)
[fdata,fdesc,fsym,flfr,Vloo,CI]=koala(X2,Y2,names,[],koala_options);

----------------------------------------------------------------------
Systems Modeling Analysis and Control (SMAC) Toolbox
APRICOT Library Version 1.0 - April 2014
Rational approximation using Surrogate Modeling
----------------------------------------------------------------------
Number of samples: 2501
Number of explanatory variables: 2
Criterion target required for the approximation function: 2.0e-007
Init swarm 1
Topology #1 --> best result 2.229230e-004 got by swarm 1
1 Kernels --> Errors: LOO =2.229230e-004 / 1.051989e-003 - Mean =2.228195e-004 / 1.051989e-003
Topology #1 --> best result 9.065491e-005 got by swarm 1
2 Kernels --> Errors: LOO =9.065491e-005 / 2.229230e-004 - Mean =9.049396e-005 / 2.228195e-004
Topology #1 --> best result 5.113924e-005 got by swarm 1
3 Kernels --> Errors: LOO =5.113924e-005 / 9.065491e-005 - Mean =5.100430e-005 / 9.049396e-005
SNLS global optimization step...
SNLS result --> Errors: LOO =2.095393e-005 - Mean =2.089645e-005
Topology #1 --> best result 1.434250e-005 got by swarm 1
4 Kernels --> Errors: LOO =1.434250e-005 / 2.095393e-005 - Mean =1.430150e-005 / 2.089645e-005
Topology #1 --> best result 8.682162e-006 got by swarm 1
5 Kernels --> Errors: LOO =8.682162e-006 / 1.434250e-005 - Mean =8.652181e-006 / 1.430150e-005
Topology #1 --> best result 7.032420e-006 got by swarm 1
6 Kernels --> Errors: LOO =7.032420e-006 / 8.682162e-006 - Mean =7.002612e-006 / 8.652181e-006
SNLS global optimization step...
SNLS result --> Errors: LOO =1.612177e-006 - Mean =1.604921e-006
Topology #1 --> best result 9.453310e-007 got by swarm 1
7 Kernels --> Errors: LOO =9.453310e-007 / 1.612177e-006 - Mean =9.392558e-007 / 1.604921e-006
Topology #1 --> best result 8.055419e-007 got by swarm 1
8 Kernels --> Errors: LOO =8.055419e-007 / 9.453310e-007 - Mean =7.993404e-007 / 9.392558e-007
Topology #1 --> best result 6.869488e-007 got by swarm 1
9 Kernels --> Errors: LOO =6.869488e-007 / 8.055419e-007 - Mean =6.812759e-007 / 7.993404e-007
SNLS global optimization step...
SNLS result --> Errors: LOO =5.162741e-007 - Mean =5.115856e-007
Topology #1 --> best result 4.838866e-007 got by swarm 1
10 Kernels --> Errors: LOO =4.838866e-007 / 5.162741e-007 - Mean =4.788427e-007 / 5.115856e-007
Topology #1 --> best result 3.432961e-007 got by swarm 1
11 Kernels --> Errors: LOO =3.432961e-007 / 4.838866e-007 - Mean =3.395193e-007 / 4.788427e-007
Topology #1 --> best result 2.978642e-007 got by swarm 1
12 Kernels --> Errors: LOO =2.978642e-007 / 3.432961e-007 - Mean =2.939332e-007 / 3.395193e-007
SNLS global optimization step...
SNLS result --> Errors: LOO =2.972808e-007 - Mean =2.933540e-007
Topology #1 --> best result 2.615813e-007 got by swarm 1
13 Kernels --> Errors: LOO =2.615813e-007 / 2.972808e-007 - Mean =2.580391e-007 / 2.933540e-007
Topology #1 --> best result 2.331112e-007 got by swarm 1
14 Kernels --> Errors: LOO =2.331112e-007 / 2.615813e-007 - Mean =2.298260e-007 / 2.580391e-007
Topology #1 --> best result 2.102054e-007 got by swarm 1
15 Kernels --> Errors: LOO =2.102054e-007 / 2.331112e-007 - Mean =2.065939e-007 / 2.298260e-007
SNLS global optimization step...
SNLS result --> Errors: LOO =1.139299e-007 - Mean =1.123123e-007
Topology #1 --> best result 8.835595e-008 got by swarm 1
16 Kernels --> Errors: LOO =8.835595e-008 / 1.139299e-007 - Mean =8.687648e-008 / 1.123123e-007
15 Kernels created !
SNLS global optimization step... CPU time for the koala call = 25.3 seconds
Size of the LFR: (trial#1 --> 60/ trial#2 --> 60) ==> Minimum size = 60
Symbolic expression of the rational approximation:
(-0.145796)/(7.60001+3.57473*Ma^2-0.104405*Ma+0.00845554*Al^2-0.472441*Al)
+(9.52858)/(3.01414+2.77778*Ma^2-3.09336*Ma+0.00468973*Al^2-0.147064*Al)
+(-9.45231)/(3.04345+2.81494*Ma^2-3.1413*Ma+0.00475151*Al^2-0.148934*Al)
+(-0.0936086)/(4.97155+6.94615*Ma^2-8.03891*Ma+0.00164671*Al^2-0.104114*Al)
+(-0.0622886)/(3.76091+3.13887*Ma^2-0.408989*Ma+0.0125134*Al^2-0.370847*Al)
+(0.0139511)/(15.0832+12.4613*Ma^2-24.6654*Ma+0.0050961*Al^2+0.195642*Al)
+(0.00771178)/(1.23571+2.77778*Ma^2-1.53683*Ma+0.477849*Al^2+0.210336*Al)
+(0.00574207)/(3.42343+3.40955*Ma^2-1.78329*Ma+0.00486616*Al^2+0.206476*Al)
+(-0.00582076)/(227.501+623.562*Ma^2-748.249*Ma+0.00237347*Al^2-0.138943*Al)
+(-0.0119818)/(3.61124+18.5892*Ma^2-10.3077*Ma+0.00278155*Al^2-0.114695*Al)
+(-0.0046268)/(201.249+3.7411*Ma^2-2.8125*Ma+0.890861*Al^2-26.6776*Al)
+(0.0227098)/(3.75475+4.52113*Ma^2-4.74905*Ma+0.00126017*Al^2-0.0871753*Al)
+(0.0581628)/(15.7129+5.57151*Ma^2-0.455403*Ma+0.0195497*Al^2-1.07229*Al)
+(0.0140545)/(168.954+152.042*Ma^2-295.391*Ma+0.0209322*Al^2-1.43169*Al)
+(-0.00621434)/(22.9791+7.00119*Ma^2-8.67755*Ma+0.0337202*Al^2-1.61303*Al)

% compute estimation errors on a rough grid
eps=Y2-fdata; sse=eps*eps'; std=sqrt(sse/length(eps)); [maxerr,kmax]=max(abs(eps));
fprintf('Estimation errors : Global=%e - RMS=%e - Max local=%e\n',sse,std,maxerr); %
plot 3D surfaces and compute validation errors on a fine grid
plosurfaces(fsym,X2,Y2,names,Xv,Yv,Vloo,CI);

Estimation errors : Global=1.591950e-004 - RMS=2.522945e-004 - Max local=1.125067e-003
Validation errors : Global=3.481691e-004 - RMS=2.738983e-004 - Max local=1.457626e-003

$\Rightarrow$ with RBF-type kernels, about two times the number of kernels is required to get a similarly accurate result, as the one got with LLM-type kernels...

Approximation and validation results (RBF model/degree 30)

Run #4: fine approximation of 2 output functions of the 16th degree

% approximation on a rough grid with koala
maxdeg=16; % degree of the rational approximation (creates maxdeg/2 kernels)
clear koala_options
koala_options.rbf=0; % LLM type (Local Linear Model)
koala_options.snls=-2; % nb of iterations between SNLS stages (negative to speed up SNLS)
koala_options.Xci=X2; % used to compute the confidence intervals
[fdata,fdesc,fsym,flfr,Vloo,CI]=koala(X2,Y2x2,names,maxdeg,koala_options);

----------------------------------------------------------------------
Systems Modeling Analysis and Control (SMAC) Toolbox
APRICOT Library Version 2.0 - September 2015
Rational approximation using Surrogate Modeling
----------------------------------------------------------------------
Number of samples: 2501
Number of explanatory variables: 2
Maximum degree required for the approximation function: 16
Init swarm 1
Topology #1 --> best result 7.810441e-005 got by swarm 1
1 Kernels --> Errors: LOO =7.810441e-005 / 7.444080e-004 - Mean =7.788438e-005 / 7.444080e-004
Topology #1 --> best result 1.955194e-005 got by swarm 1
2 Kernels --> Errors: LOO =1.955194e-005 / 7.810441e-005 - Mean =1.944049e-005 / 7.788438e-005
SNLS global optimization step...
SNLS result --> Errors: LOO =1.228991e-005 - Mean =1.222416e-005
Topology #1 --> best result 7.550309e-006 got by swarm 1
3 Kernels --> Errors: LOO =7.550309e-006 / 1.228991e-005 - Mean =7.493907e-006 / 1.222416e-005
Topology #1 --> best result 3.864809e-006 got by swarm 1
4 Kernels --> Errors: LOO =3.864809e-006 / 7.550309e-006 - Mean =3.827405e-006 / 7.493907e-006
SNLS global optimization step...
SNLS result --> Errors: LOO =1.858792e-006 - Mean =1.841368e-006
Topology #1 --> best result 1.292434e-006 got by swarm 1
5 Kernels --> Errors: LOO =1.292434e-006 / 1.858792e-006 - Mean =1.275457e-006 / 1.841368e-006
Topology #1 --> best result 1.027822e-006 got by swarm 1
6 Kernels --> Errors: LOO =1.027822e-006 / 1.292434e-006 - Mean =1.010716e-006 / 1.275457e-006
SNLS global optimization step...
SNLS result --> Errors: LOO =5.566995e-007 - Mean =5.475250e-007
Topology #1 --> best result 4.332944e-007 got by swarm 1
7 Kernels --> Errors: LOO =4.332944e-007 / 5.566995e-007 - Mean =4.246384e-007 / 5.475250e-007
Topology #1 --> best result 3.699539e-007 got by swarm 1
8 Kernels --> Errors: LOO =3.699539e-007 / 4.332944e-007 - Mean =3.616834e-007 / 4.246384e-007
Max nb of Kernels reached 8 !
SNLS global optimization step...
SNLS result --> Errors: LOO =3.030156e-007 - Mean =2.965075e-007
CPU time for the koala call = 37.05
Size of the LFR: 32
Symbolic expression of the rational approximation #1:
(1.55042-1.41912*Ma-0.0831038*Al)/(3.5751+2.77789*Ma^2-1.76935*Ma+0.00919257*Al^2-0.290392*Al)
+(0.398047-0.867761*Ma+0.0386589*Al)/(2.34039+3.47406*Ma^2-3.96301*Ma+0.00100666*Al^2-0.0290922*Al)
+(-1.44146+1.32124*Ma+0.0780251*Al)/(3.88487+2.79582*Ma^2-1.62705*Ma+0.0100532*Al^2-0.326327*Al) +(-0.372527+0.713121*Ma-0.0211241*Al)/(3.09913+4.35158*Ma^2-5.48545*Ma+0.000987738*Al^2-0.0382565*Al)
+(0.0153159-0.0135557*Ma-0.000620656*Al)/(2.07113+2.77782*Ma^2-3.44303*Ma+0.44384*Al^2+0.0867833*Al)
+(-0.169486+0.37575*Ma-0.0183432*Al)/(1.69792+2.86543*Ma^2-2.61671*Ma+0.00107865*Al^2-0.020826*Al)
+(-0.0115804+0.0103921*Ma-1.19719e-005*Al)/(265.679+721.188*Ma^2-870.724*Ma+0.00357897*Al^2-0.163307*Al)
+(-0.0933428+0.0852677*Ma+0.00217524*Al)/(22.9016+22.1174*Ma^2-43.7919*Ma+0.00761736*Al^2-0.082788*Al)
Symbolic expression of the rational approximation #2:
(0.942669-1.04931*Ma-0.0505198*Al)/(3.5751+2.77789*Ma^2-1.76935*Ma+0.00919257*Al^2-0.290392*Al)
+(0.622765-0.00278502*Ma+0.0138056*Al)/(2.34039+3.47406*Ma^2-3.96301*Ma+0.00100666*Al^2-0.0290922*Al)
+(-0.908564+0.987944*Ma+0.0474548*Al)/(3.88487+2.79582*Ma^2-1.62705*Ma+0.0100532*Al^2-0.326327*Al)
+(-0.710695+0.449448*Ma-0.00567226*Al)/(3.09913+4.35158*Ma^2-5.48545*Ma+0.000987738*Al^2-0.0382565*Al)
+(0.0134368-0.0126297*Ma-0.000376396*Al)/(2.07113+2.77782*Ma^2-3.44303*Ma+0.44384*Al^2+0.0867833*Al)
+ (-0.058788-0.227182*Ma-0.00657102*Al)/(1.69792+2.86543*Ma^2-2.61671*Ma+0.00107865*Al^2-0.020826*Al)
+(-0.021775+0.0316405*Ma-6.30015e-005*Al)/(265.679+721.188*Ma^2-870.724*Ma+0.00357897*Al^2-0.163307*Al)
+(-0.0699683+0.0670589*Ma+0.00105827*Al)/(22.9016+22.1174*Ma^2-43.7919*Ma+0.00761736*Al^2-0.082788*Al)

for j=1:2
% compute errors on the estimation grid
eps=Y2x2(j,:)-fdata(j,:); sse=eps*eps'; std=sqrt(sse/length(eps)); [maxerr,kmax]=max(abs(eps));
fprintf('Estimation errors : Global=%e - RMS=%e - Max local=%e\n',sse,std,maxerr);
% plot 3D surfaces and compute errors on the validation grid
% plot output variances (LOO-type) on the rough estimation grid
% via a color map (continuous transition from green for lower values to red for upper values)
% plot 3D Confidence Intervals on a fine validation grid
if j==1, options.viewpoint=[0 0]; else, options.viewpoint=[25 25]; end
plosurfaces(fsym(j),X2,Y2x2(j,:),names,X2,Y2x2(j,:),Vloo(j,:),CI(j,:),options);
end

Estimation errors of the rational approximation #1: Global=6.219525e-004 - RMS=4.986798e-004 - Max local=2.702094e-003
Validation errors of the rational approximation #1: Global=6.220166e-004 - RMS=4.987055e-004 - Max local=2.699280e-003

Approximation/validation results for output #1 (LLM model/degree 16)

Estimation errors of the rational approximation #2: Global=8.611781e-004 - RMS=5.867994e-004 - Max local=3.569869e-003
Validation errors of the rational approximation #2: Global=8.611518e-004 - RMS=5.867904e-004 - Max local=3.566210e-003

Approximation/validation results for output #2 (LLM model/degree 16)

Output variance and Confidence Intervals (LLM model/degree 16)

Run #5: very rough approximation of 2 output functions of the 16th degree $\hspace{0.35cm}$(with deliberately degraded data: under-sampling, truncated domain, noise)

% approximation on a rough grid with koala
maxdeg=16; % degree of the rational approximation (creates maxdeg/2 kernels)
clear koala_options
koala_options.rbf=0; % LLM type (Local Linear Model)
koala_options.snls=-2; % nb of iterations between SNLS stages (negative to speed up SNLS)
koala_options.Xci=Xv; % used to compute the confidence intervals
[fdata,fdesc,fsym,flfr,Vloo,CI]=koala(X3,Y3,names,maxdeg,koala_options);

----------------------------------------------------------------------
Systems Modeling Analysis and Control (SMAC) Toolbox
APRICOT Library Version 2.0 - September 2015
Rational approximation using Surrogate Modeling
----------------------------------------------------------------------
Number of samples: 504
Number of explanatory variables:2
Maximum degree required for the approximation function: 16
Init swarm 1 Topology #1 --> best result 5.961742e-005 got by swarm 1
1 Kernels --> Errors: LOO =5.961742e-005 / 6.903073e-004 - Mean =5.879257e-005 / 6.903073e-004
Topology #1 --> best result 1.276681e-005 got by swarm 1
2 Kernels --> Errors: LOO =1.276681e-005 / 5.961742e-005 - Mean =1.241782e-005 / 5.879257e-005
SNLS global optimization step...
SNLS result --> Errors: LOO =9.879487e-006 - Mean =9.621677e-006
Topology #1 --> best result 6.933679e-006 got by swarm 1
3 Kernels --> Errors: LOO =6.933679e-006 / 9.879487e-006 - Mean =6.686358e-006 / 9.621677e-006
Topology #1 --> best result 4.816125e-006 got by swarm 1
4 Kernels --> Errors: LOO =4.816125e-006 / 6.933679e-006 - Mean =4.586268e-006 / 6.686358e-006
SNLS global optimization step...
SNLS result --> Errors: LOO =3.245626e-006 - Mean =3.100728e-006
Topology #1 --> best result 2.869053e-006 got by swarm 1
5 Kernels --> Errors: LOO =2.869053e-006 / 3.245626e-006 - Mean =2.698204e-006 / 3.100728e-006
Topology #1 --> best result 2.703614e-006 got by swarm 1
6 Kernels --> Errors: LOO =2.703614e-006 / 2.869053e-006 - Mean =2.511407e-006 / 2.698204e-006
SNLS global optimization step...
SNLS result --> Errors: LOO =2.651120e-006 - Mean =2.462729e-006
Topology #1 --> best result 2.564660e-006 got by swarm 1
7 Kernels --> Errors: LOO =2.564660e-006 / 2.651120e-006 - Mean =2.352161e-006 / 2.462729e-006
Topology #1 --> best result 2.456852e-006 got by swarm 1
8 Kernels --> Errors: LOO =2.456852e-006 / 2.564660e-006 - Mean =2.224895e-006 / 2.352161e-006
Max nb of Kernels reached 8 !
SNLS global optimization step...
SNLS result --> Errors: LOO =2.450429e-006 - Mean =2.218599e-006
SNLS result --> Errors: LOO =2.450429e-006 - Mean =2.218599e-006
CPU time for the koala call = 7.62
Size of the LFR: 32
Symbolic expression of the rational approximation #1:
(0.723874-0.869818*Ma-0.0437871*Al)/(3.14769+3.43948*Ma^2-3.00811*Ma+0.00587584*Al^2-0.187135*Al)
+(-0.207699+0.216441*Ma+0.00889581*Al)/(4.00976+4.37439*Ma^2-6.37982*Ma+0.0025022*Al^2-0.0827166*Al)
+(-0.601723+0.825851*Ma+0.0341526*Al)/(3.51563+3.96043*Ma^2-3.03588*Ma+0.00697956*Al^2-0.232356*Al)
+(0.0391634-0.00560088*Ma-0.00363129*Al)/(6.49565+8.73483*Ma^2-12.1344*Ma+0.00143731*Al^2-0.0858322*Al)
+(0.016745-0.00841147*Ma+0.00691492*Al)/(5.519+3.44145*Ma^2-5.51833*Ma+1.73308*Al^2+3.99899*Al)
+(-2.65002e-005-0.0150338*Ma-0.000395485*Al)/(20.4442+41.2294*Ma^2-29.0451*Ma+0.0679094*Al^2+1.97288*Al)
+(-0.0480629+0.0264305*Ma+0.000671782*Al)/(1247.41+3.42936*Ma^2-2.41307*Ma+5.53633*Al^2-166.11*Al)
+(-0.0468953+0.0390371*Ma+0.000310454*Al)/(5160.43+14226.7*Ma^2-17112.3*Ma+0.0146655*Al^2-0.893556*Al)
Symbolic expression of the rational approximation #2:
(1.19996-1.41983*Ma-0.0445534*Al)/(3.14769+3.43948*Ma^2-3.00811*Ma+0.00587584*Al^2-0.187135*Al)
+(-0.123002+0.287273*Ma+0.00507312*Al)/(4.00976+4.37439*Ma^2-6.37982*Ma+0.0025022*Al^2-0.0827166*Al)
+(-1.06396+1.18861*Ma+0.0398442*Al)/(3.51563+3.96043*Ma^2-3.03588*Ma+0.00697956*Al^2-0.232356*Al)
+(-0.108137+0.090931*Ma-0.0003866*Al)/(6.49565+8.73483*Ma^2-12.1344*Ma+0.00143731*Al^2-0.0858322*Al)
+(0.0178377-0.0101732*Ma+0.00583077*Al)/(5.519+3.44145*Ma^2-5.51833*Ma+1.73308*Al^2+3.99899*Al)
+(0.013111-0.0366002*Ma+0.000206088*Al)/(20.4442+41.2294*Ma^2-29.0451*Ma+0.0679094*Al^2+1.97288*Al)
+(-0.0556314-0.00276016*Ma+0.00320701*Al)/(1247.41+3.42936*Ma^2-2.41307*Ma+5.53633*Al^2-166.11*Al)
+(-0.112677+0.185593*Ma-0.000468049*Al)/(5160.43+14226.7*Ma^2-17112.3*Ma+0.0146655*Al^2-0.893556*Al)

for j=1:2
% compute errors on the estimation grid
eps=Y3(j,:)-fdata(j,:); sse=eps*eps'; std=sqrt(sse/length(eps)); [maxerr,kmax]=max(abs(eps)); fprintf('Estimation errors : Global=%e - RMS=%e - Max local=%e\n',sse,std,maxerr);
% plot 3D surfaces and compute errors on the validation grid
% plot output variances (LOO-type) on the very rough estimation grid
% via a color map (continuous transition from green for lower values to red for upper values)
% plot 3D Confidence Intervals on a fine validation grid
if j==1, options.viewpoint=[0 0]; else, options.viewpoint=[25 25]; end
plosurfaces(fsym(j),X3,Y3(j,:),names,Xv,Yvx2(j,:),Vloo(j,:),CI(j,:),options);
end

Estimation errors of the rational approximation #1: Global=1.020212e-003 - RMS=1.422754e-003 - Max local=3.621021e-003
Validation errors of the rational approximation #1: Global=5.814002e-002 - RMS=3.539418e-003 - Max local=2.201596e-002

Approx./validation results for output #1 (LLM model/degree 16/poor data)

Estimation errors of the rational approximation #2: Global=1.216136e-003 - RMS=1.553373e-003 - Max local=3.913035e-003
Validation errors of the rational approximation #2: Global=3.263002e-002 - RMS=2.651569e-003 - Max local=9.148029e-003

Approx./validation results for output #2 (LLM model/degree 16/poor data)

Output variance and Confidence Intervals (LLM model/degree 16/poor data)

References

[1]	A. Bucharles et al., "An overview of relevant issues for aircraft model identification", AerospaceLab, Issue 4, http://www.aerospacelab-journal.org/al4, 2012.
[2]	S. Chen, X. Hong, C.J. Harris and P.M. Sharkey, "Sparse modelling using orthogonal forward regression with PRESS statistic and regularization", IEEE Transactions on Systems, Man and Cybernetics (B), 34 (2), pp. 898-911, 2004.
[3]	S. Chen, X. Hong, B.L. Luk and C.J. Harris, "Non-linear system identification using particle swarm optimization tuned radial basis function models", International Journal of Bio-Inspired Computation, 1 (4), pp. 246-258, 2009.
[4]	M. Clerc, "Particle swarm optimization", ISTE, London, 2006.
[5]	G. Hardier, "Recurrent RBF networks for suspension system modeling and wear diagnosis of a damper", IEEE World Congress on Computational Intelligence, 3, pp. 2441-2446, Anchorage, USA, 1998.
[6]	G. Hardier, C. Roos and C. Seren, "Creating sparse rational approximations for linear fractional representations using surrogate modeling", in Proceedings of the 3rd IFAC International Conference on Intelligent Control and Automation Science, Chengdu, China, pp. 238-243, September 2013.
[7]	S. Haykin, "Neural Networks: A Comprehensive Foundation", IEEE Press, MacMillan, New York, 1994.
[8]	E.A. Morelli and R. DeLoach, "Wind tunnel database development using modern experiment design and multivariate orthogonal functions", 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, USA, 2003.
[9]	O. Nelles and R. Isermann, "Basis function networks for interpolation of local linear models", 35th IEEE Conference on Decision and Control, pp. 470-475, Kobe, Japan, 1996.
[10]	C. Seren, G. Hardier and P. Ezerzere, "On-line Estimation of Longitudinal Flight Parameters", SAE AeroTech Congress and Exhibition, Toulouse, France, 2011.