Routine display_sector

Display a truncated sector.

Description

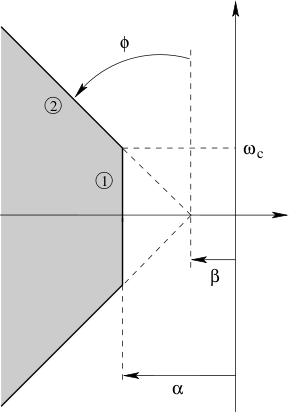
This routine displays a truncated sector in the complex plane. If requested by the user, the eigenvalues of a given LTI system can be displayed too. With reference to the figure below, a truncated sector is defined by three parameters :

The relative stability degree $\alpha$ is the distance between the vertical axis and segment 1. It is negative if segment 1 is inside the left half plane.
The angle between the vertical axis and segment 2 is denoted $\phi$ . It is positive if segment 2 is generated by an anticlockwise rotation of the vertical axis. If $\beta=0$ , $\xi=sin(\phi)$ corresponds to the damping factor.
The imaginary part of the intersection point between segments 1 and 2 is denoted $\omega_c$ . It is always positive. If omitted, it is automatically computed so that $\beta=0$ .

Syntax

display_sector(sector{,sys})

Input arguments

`sector`	Vector [ $\alpha$ $\xi$ $\omega_c$ ] characterizing the considered truncated sector. The third parameter $\omega_c$ is optional. If omitted, its value is automatically computed so that $\beta=0$ .
`sys`	LTI object or square matrix whose eigenvalues are to be plotted. A list of eigenvalues can also be directly given. This argument is optional and the default value is `sys=[]`.

Example

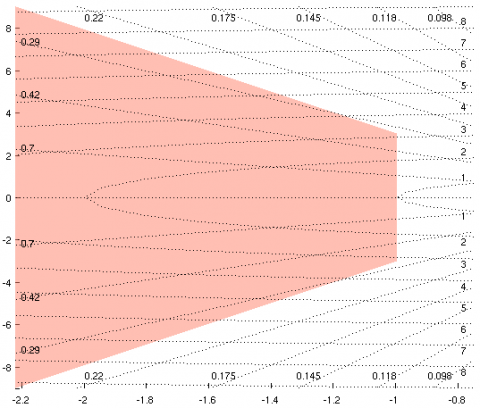
sector=[-1 0.2 3]; display_sector(sector);

Description

Syntax

Input arguments

Example

See also