Routine muub_lmi

Compute (skew-)$\mu$ upper bounds on a grid with LMI tools.

Description

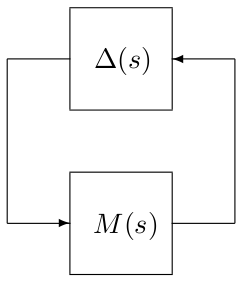
This routine computes a (skew-)$\mu$ upper bound for an interconnection between a nominal LTI system $M(s)$ and a block-diagonal operator $\Delta(s)= diag\left(\Delta_1(s),\dots,\Delta_N(s)\right)$. The bound is computed on a frequency grid $(\omega_k)_{k\in [1,m]}$ and the resulting $D$ and $G$ scaling matrices have the same values for all frequency points.

stab

Syntax

[ubnd,D,G,S]=muub_lmi(M,blk{,options})

Input arguments

The first two input arguments are mandatory:

M2-D or 3-D numeric array describing the LTI system $M(s)$. M(:,:,k) corresponds to the frequency response $M(j\omega_k)$.
blk

Matrix defining the structure of the block-diagonal operator $\Delta(s)=diag\left(\Delta_1(s),...,\Delta_N(s)\right)$. Its first 2 columns must be defined as follows for all $i=1,...,N$:

  • blk(i,1:2)=[-ni 0] $\Rightarrow$ $\Delta_i(s)=\delta_iI_{n_i}$ with $\delta_i$ real,
  • blk(i,1:2)=[ni 0] $\Rightarrow$ $\Delta_i(s)=\delta_iI_{n_i}$ with $\delta_i$ complex,
  • blk(i,1:2)=[ni ni] $\Rightarrow$ $\Delta_i(s)$ is a $n_i\times n_i$ LTI system.

A third column can be used to specify skew uncertainties:

  • blk(i,3)=0 $\Rightarrow$ $\overline{\sigma}(\Delta_i(j\omega_k))\le 1$ for all $k=1,\dots,m$,
  • blk(i,3)=1 $\Rightarrow$ $\overline{\sigma}(\Delta_i(j\omega_k))\le 1/$ubnd for all $k=1,\dots,m$, where ubnd is minimized.

If none, blk(i,3) is set to 1 for all $i=1,...,N$.

The third input argument options is an optional structured variable with fields:

targetThe LMI solver stops if the (skew-)$\mu$ upper bound becomes lower than target. The default value is options.target=0.
epsilonThe constraint $D>\epsilon I$ is considered instead of $D>0$. The default value is options.epsilon=1e-8.
lmioptTuning parameters of the LMI solver (see the routine gevp or mincx of the Robust Control Toolbox). The default value is options.lmiopt=[0.02 100 1e10 5 1].

Output arguments

ubnd(Skew-)$\mu$ upper bound $\beta$.
D$D$ scaling matrix.
G$G$ scaling matrix.
S$S$ matrix (for skew-$\mu$ problems only).

In case of a classical $\mu$ problem, the output arguments satisfy: $$M^*(j\omega_k)DM(j\omega_k)+j(GM(j\omega_k)-M^*(j\omega_k)G)\le\beta^2D\ \ \ \textrm{for all}\ \ \ k=1,\dots,m$$ where the $\mu$ upper bound $\beta$ is minimized. In case of a skew-$\mu$ problem, the output arguments satisfy: $$M^*(j\omega_k)DM(j\omega_k)+j(GM(j\omega_k)-M^*(j\omega_k)G)\le S(\beta)D\ \ \ \textrm{for all}\ \ \ k=1,\dots,m$$ where the skew-$\mu$ upper bound $\beta$ is minimized, and $S(\beta)=diag\left(S_1(\beta),\dots,S_N(\beta)\right)$ is a block-diagonal matrix such that:

  • $S_i(\beta)=I_{n_i}$ if blk(i,3)=0,
  • $S_i(\beta)=\beta^2I_{n_i}$ if blk(i,3)=1.

Examples

sys=rss(20,14,14)/10;
M=freqresp(sys,1:5);

1. Computation of a $\mu$ upper bound blk=[-2 0 1;3 0 1;3 3 1;-1 0 1;1 0 1;1 1 1;-3 0 1];
[ubnd,D,G]=muub_lmi(M,blk);ubnd
for k=1:5
$\ \ \ $ max(real(eig(M(:,:,k)'*D*M(:,:,k)+1i*(G*M(:,:,k)-M(:,:,k)'*G)-ubnd^2*D)))
end
All eigenvalues are negative at each considered frequency.

2. Computation of a skew-$\mu$ upper bound blk=[-2 0 0;3 0 0;3 3 1;-1 0 0;1 0 1;1 1 0;-3 0 1];
[ubnd,D,G,S]=muub_lmi(M,blk);ubnd
for k=1:5
$\ \ \ $ max(real(eig(M(:,:,k)'*D*M(:,:,k)+1i*(G*M(:,:,k)-M(:,:,k)'*G)-S*D)))
end
All eigenvalues are negative at each considered frequency.

See also

muub
muub_mixed