Routine make_square

Make all uncertainty blocks square.

Description

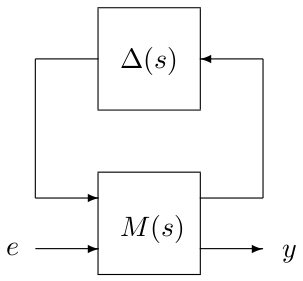
This routine transforms the interconnection of the figure below so that the block-diagonal operator $\Delta(s)$ is only composed of square blocks. For example, if the initial size of the ith block $\Delta_i(s)$ of $\Delta(s)$ is $n_i\times m_i$, then:

  • $m_i-n_i\ $ zero inputs are added to $M(s)$ if $m_i>n_i$,
  • $n_i-m_i\ $ zero outputs are added to $M(s)$ if $n_i>m_i$.
perf

Syntax

[sys2,blk2]=make_square(sys,blk{,perfo})

Input arguments

sysLTI object describing $M(s)$. It can also be a 2-D or a 3-D numeric array corresponding to the frequency response of $M(s)$ on a grid.
blk

Matrix defining the structure of the block-diagonal operator $\Delta(s)=diag\left(\Delta_1(s),...,\Delta_N(s)\right)$. Its first 2 columns must be defined as follows for all $i=1,...,N$:

  • blk(i,1:2)=[-ni 0] $\Rightarrow$ $\Delta_i(s)=\delta_iI_{n_i}$ with $\delta_i$ real,
  • blk(i,1:2)=[ni 0] $\Rightarrow$ $\Delta_i(s)=\delta_iI_{n_i}$ with $\delta_i$ complex,
  • blk(i,1:2)=[ni mi] $\Rightarrow$ $\Delta_i(s)$ is a $n_i\times m_i$ LTI system.
perfoIf nonzero, the performance channel between e and y (if any) is also made square. This argument is optional and the default value is perfo=0.

Output arguments

The interconnection defined by sys2 and blk2 is equivalent to the one described by sys and blk from an input/output point of view, but $\Delta(s)$ is now only composed of square blocks.

Example

sys=rss(2,5,4);
blk=[-1 0;2 1];
[sys2,blk2]=make_square(sys,blk,0)
A zero output associated to the second block is added.
[sys2,blk2]=make_square(sys,blk,1)
Two zero inputs associated to the performance channel are added.